题目内容
13.某一时刻甲、乙两木杆的影子长分别是2米和3米,已知乙杆的高度是1.5米,则甲杆的高度是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 设甲杆的高度为xm,利用在同一时刻物高与影长的比相等得$\frac{x}{2}$=$\frac{1.5}{3}$,然后解方程即可.
解答 解:设甲杆的高度为xm,
根据题意得$\frac{x}{2}$=$\frac{1.5}{3}$,解得x=1,
即甲杆的高度是1m.
故选A.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度.通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
3.下列说法中正确的是( )
| A. | -42表示(-4)×(-4) | B. | -8没有立方根 | C. | $\sqrt{5}$与$-\sqrt{5}$是相反数 | D. | 64的平方根是8 |
4.已知线段AB的长为6 cm,点P是线段AB的黄金分割点,则PA的长为(单位:cm)( )
| A. | $3\sqrt{5}-3$ | B. | $9-3\sqrt{5}$或$6-3\sqrt{5}$ | C. | $3\sqrt{5}-3$或$9-3\sqrt{5}$ | D. | $6-3\sqrt{5}$ |
1.把多项式(x+1)(x-1)-(1-x)提取公因式(x-1)后,余下的部分是( )
| A. | (x+1) | B. | (x-1) | C. | x | D. | (x+2) |
8.25的平方根是( )
| A. | ±5 | B. | 5 | C. | ±$\sqrt{5}$ | D. | -5 |
18.下列结论正确的是( )
| A. | 有理数包括正数和负数 | B. | 数轴上原点两侧的数互为相反数 | ||
| C. | 0是绝对值最小的数 | D. | 倒数等于本身的数是0、1、-1 |
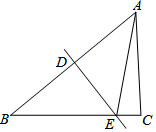 如图,在Rt△ABC中,∠ACB=90°,斜边AB的垂直平分线交AB于点D,交BC于点E.已知AB=5,AC=3,则△ACE的周长为( )
如图,在Rt△ABC中,∠ACB=90°,斜边AB的垂直平分线交AB于点D,交BC于点E.已知AB=5,AC=3,则△ACE的周长为( )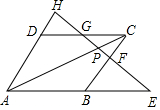 如图,过?ABCD的对角线AC上任一点P作一直线,分别交AB、BC、CD、DA所在直线于E、F、G、H.求证:PE•PF=PG•PH.
如图,过?ABCD的对角线AC上任一点P作一直线,分别交AB、BC、CD、DA所在直线于E、F、G、H.求证:PE•PF=PG•PH.