题目内容
1．把多项式（x+1）（x-1）-（1-x）提取公因式（x-1）后，余下的部分是（ ）| A． | （x+1） | B． | （x-1） | C． | x | D． | （x+2） |
分析 原式变形后，提取公因式即可得到所求结果．
解答 解：原式=（x+1）（x-1）+（x-1）=（x-1）（x+2），
则余下的部分是（x+2），
故选D
点评 此题考查了公因式，熟练掌握提取公因式的方法是解本题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
11．a是一个两位数，b是一个三位数，把a放在b的右边组成一个五位数，用a，b的代数式表示所得的五位数是（ ）
| A． | ba | B． | 10b+a | C． | 10000b+a | D． | 100b+a |
12．
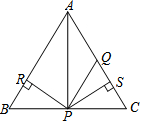如图，等腰△ABC中，AB=AC，AQ=PQ，PR=PS，PR⊥AB于点R，PS⊥AC于点S，则下列结论：①S△ABP=S△ACP；②AS=AR；③QP∥AB；④△BPR≌△QPS；⑤AQ=CQ中正确的有（ ）
如图，等腰△ABC中，AB=AC，AQ=PQ，PR=PS，PR⊥AB于点R，PS⊥AC于点S，则下列结论：①S△ABP=S△ACP；②AS=AR；③QP∥AB；④△BPR≌△QPS；⑤AQ=CQ中正确的有（ ）| A． | ①②③④ | B． | ②③④ | C． | ①③④⑤ | D． | ①②③⑤ |
9．满足下列长度的三根木棒中，能钉成一个三角形的是（ ）
| A． | 32，42，52 | B． | 1，$\sqrt{2}$，$\sqrt{3}$ | C． | 1，2，3 | D． | 12，22，32 |
16．
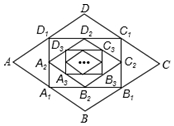如图，在菱形ABCD中，边长为10，∠A=60°．顺次连结菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连结四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连结四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；按此规律继续下去…．四边形A2nB2nC2nD2n的周长是（ ）
如图，在菱形ABCD中，边长为10，∠A=60°．顺次连结菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连结四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连结四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；按此规律继续下去…．四边形A2nB2nC2nD2n的周长是（ ）| A． | $\frac{5}{{2}^{n-2}}$ | B． | $\frac{5}{{2}^{n-3}}$ | C． | $\frac{5}{{2}^{n}}$ | D． | $\frac{5}{{2}^{n-1}}$ |
6．
将一直角三角板与两边平行的硬纸条如图所示放置，下列结论：
（1）∠1=∠2；（2）∠2+∠4=90°；（3）∠2+∠3=90°；（4）∠4+∠5=180°；（5）∠1+∠3=90°．其中正确的个数是（ ）
将一直角三角板与两边平行的硬纸条如图所示放置，下列结论：（1）∠1=∠2；（2）∠2+∠4=90°；（3）∠2+∠3=90°；（4）∠4+∠5=180°；（5）∠1+∠3=90°．其中正确的个数是（ ）
| A． | 5 | B． | 4 | C． | 3 | D． | 2 |
10．下列运算正确的是（ ）
| A． | a3+a4=a6 | B． | a3•a2=a6 | C． | （-a）5÷（-a）3=a2 | D． | （a2）3=a5 |
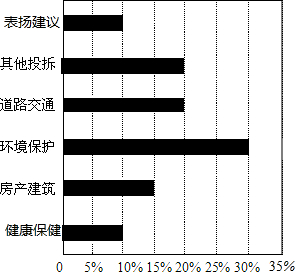如图是一家报纸“百姓热线”一周内接到热线电话的统计图，其中有关环境保护问题的电话最多，共30个．本周“百姓热线”共接到热线电话有100个．