题目内容
4．已知线段AB的长为6 cm，点P是线段AB的黄金分割点，则PA的长为（单位：cm）（ ）| A． | $3\sqrt{5}-3$ | B． | $9-3\sqrt{5}$或$6-3\sqrt{5}$ | C． | $3\sqrt{5}-3$或$9-3\sqrt{5}$ | D． | $6-3\sqrt{5}$ |
分析 根据黄金分割点的定义，当AP是较长线段时，PA=$\frac{\sqrt{5}-1}{2}$AB；当AP是较短线段时，PA=$\frac{3-\sqrt{5}}{2}$AB，分别代入AB的值，进行计算即可得出答案．
解答 解：由于P为线段AB=6的黄金分割点，
当AP是较长线段时，PA=6×$\frac{\sqrt{5}-1}{2}$=3$\sqrt{5}$-3；
当AP是较短线段时，PA=6×$\frac{3-\sqrt{5}}{2}$=9-3$\sqrt{5}$；
故选C．
点评 此题考查了黄金分割，理解黄金分割点的概念．应该识记黄金分割的公式：较短的线段=原线段的$\frac{3-\sqrt{5}}{2}$，较长的线段=原线段的$\frac{\sqrt{5}-1}{2}$．
练习册系列答案
相关题目
14．若点B在x轴下方，y轴右侧，并且到x轴、y轴距离分别是3和2个单位长度，则点B的坐标（ ）
| A． | （3，-2） | B． | （-3，2） | C． | （2，-3） | D． | （-2，-3） |
15．已知单项式-5am-1b6与$\frac{1}{2}$ab2n的和仍是单项式，则m-n的值是（ ）
| A． | 1 | B． | -1 | C． | -2 | D． | -3 |
12．
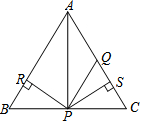如图，等腰△ABC中，AB=AC，AQ=PQ，PR=PS，PR⊥AB于点R，PS⊥AC于点S，则下列结论：①S△ABP=S△ACP；②AS=AR；③QP∥AB；④△BPR≌△QPS；⑤AQ=CQ中正确的有（ ）
如图，等腰△ABC中，AB=AC，AQ=PQ，PR=PS，PR⊥AB于点R，PS⊥AC于点S，则下列结论：①S△ABP=S△ACP；②AS=AR；③QP∥AB；④△BPR≌△QPS；⑤AQ=CQ中正确的有（ ）| A． | ①②③④ | B． | ②③④ | C． | ①③④⑤ | D． | ①②③⑤ |
19．下列表述正确的是（ ）
| A． | -（-10）＜0 | B． | （-10）2＜92 | C． | -102＜0 | D． | -（-10）2＞0 |
9．满足下列长度的三根木棒中，能钉成一个三角形的是（ ）
| A． | 32，42，52 | B． | 1，$\sqrt{2}$，$\sqrt{3}$ | C． | 1，2，3 | D． | 12，22，32 |
16．
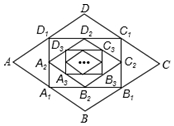如图，在菱形ABCD中，边长为10，∠A=60°．顺次连结菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连结四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连结四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；按此规律继续下去…．四边形A2nB2nC2nD2n的周长是（ ）
如图，在菱形ABCD中，边长为10，∠A=60°．顺次连结菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连结四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连结四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；按此规律继续下去…．四边形A2nB2nC2nD2n的周长是（ ）| A． | $\frac{5}{{2}^{n-2}}$ | B． | $\frac{5}{{2}^{n-3}}$ | C． | $\frac{5}{{2}^{n}}$ | D． | $\frac{5}{{2}^{n-1}}$ |
14．若a，b，c是△ABC的三边，则化简|a-b-c|-|b-a-c|的结果是（ ）
| A． | 2a-2b | B． | 2b-2a | C． | 2c | D． | 0 |