题目内容
2.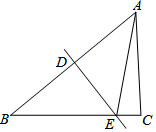 如图,在Rt△ABC中,∠ACB=90°,斜边AB的垂直平分线交AB于点D,交BC于点E.已知AB=5,AC=3,则△ACE的周长为( )
如图,在Rt△ABC中,∠ACB=90°,斜边AB的垂直平分线交AB于点D,交BC于点E.已知AB=5,AC=3,则△ACE的周长为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 根据线段的垂直平分线的性质得到AE=BE,根据勾股定理求出BC的长,根据三角形的周长公式计算即可.
解答 解:由勾股定理得,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=4,
∵DE是AB的垂直平分线,
∴AE=BE,
又∵AC=3,
∴△ACE的周长=AC+CE+AE=AC+BC=3+4=7.
故选:C.
点评 本题考查的是勾股定理,线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
12.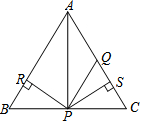 如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )
如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )
 如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )
如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )| A. | ①②③④ | B. | ②③④ | C. | ①③④⑤ | D. | ①②③⑤ |
10.下列运算正确的是( )
| A. | a3+a4=a6 | B. | a3•a2=a6 | C. | (-a)5÷(-a)3=a2 | D. | (a2)3=a5 |
7.若4x2+mxy+16y2是一个完全平方式,则m的值为( )
| A. | 8 | B. | 16 | C. | ±16 | D. | ±8 |
14.若a,b,c是△ABC的三边,则化简|a-b-c|-|b-a-c|的结果是( )
| A. | 2a-2b | B. | 2b-2a | C. | 2c | D. | 0 |
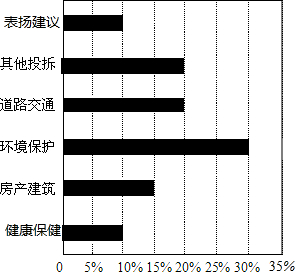 如图是一家报纸“百姓热线”一周内接到热线电话的统计图,其中有关环境保护问题的电话最多,共30个.本周“百姓热线”共接到热线电话有100个.
如图是一家报纸“百姓热线”一周内接到热线电话的统计图,其中有关环境保护问题的电话最多,共30个.本周“百姓热线”共接到热线电话有100个.