题目内容
3.计算:(1)因式分解:
①2ax2-18ay2
②(a+b)2-12a-12b+36
(2)解不等式组$\left\{\begin{array}{l}{3x-2<2x+2}\\{6-x≥1-3(x-1)}\end{array}\right.$
(3)解方程:$\frac{2-x}{3+x}$=$\frac{1}{2}$+$\frac{1}{x+3}$.
分析 (1)根据提公因式法以及公式法进行因式分解即可;
(2)先求出其中各不等式的解集,再求出这些解集的公共部分;
(3)解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.
解答 解:(1)①2ax2-18ay2
=2a(x2-9y2 )
=2a(x+3y)(x-3y);
②(a+b)2-12a-12b+36
=(a+b)2-12(a+b)+36
=(a+b-6)2;
(2)$\left\{\begin{array}{l}{3x-2<2x+2①}\\{6-x≥1-3(x-1)②}\end{array}\right.$
解不等式①,可得x<4,
解不等式②,可得x≥-1,
∴不等式组的解集为-1≤x<4;
(3)$\frac{2-x}{3+x}$=$\frac{1}{2}$+$\frac{1}{x+3}$
两边同乘2(x+3),可得
2(2-x)=x+3+2
解得x=-$\frac{1}{3}$,
经检验,x=-$\frac{1}{3}$是原方程的解.
点评 本题主要考查了因式分解、解一元一次不等式组以及解分式方程,解题时注意:解分式方程时,去分母后所得整式方程的解有可能使原方程中的分母为0,所以应检验.

练习册系列答案
相关题目
10.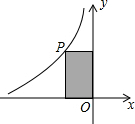 如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )
如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )
 如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )
如图,点P时反比例函数y=$\frac{k}{x}$图象上一点,过点P分别作x轴、y轴的垂线段,与坐标轴围成的矩形面积是4,那么反比例函数的解析式是( )| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{2}{x}$ | C. | y=$\frac{4}{x}$ | D. | y=-$\frac{4}{x}$ |
14.因式分解x3-2x2+x正确的是( )
| A. | (x-1)2 | B. | x (x-1)2 | C. | x( x2-2x+1) | D. | x (x+1)2 |
11.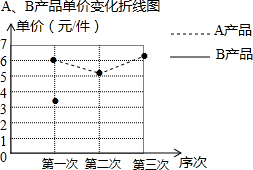 某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.
某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.
A,B产品单价变化统计表
并求得了A产品三次单价的平均数和方差:
$\overline{{x}_{A}}$=5.9,SA2=$\frac{1}{3}$[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=$\frac{43}{150}$
(1)在折线图中画出B产品的单价变化的情况;
(2)求B产品三次单价的方差;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件的基础上调m%(m>0),但调价后不能超过4元/件,并且使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
 某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.
某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.A,B产品单价变化统计表
| 第一次 | 第二次 | 第三次 | |
| A产品单价(元/件) | 6 | 5.2 | 6.5 |
| B产品单价(元/件) | 3.5 | 4 | 3 |
$\overline{{x}_{A}}$=5.9,SA2=$\frac{1}{3}$[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=$\frac{43}{150}$
(1)在折线图中画出B产品的单价变化的情况;
(2)求B产品三次单价的方差;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件的基础上调m%(m>0),但调价后不能超过4元/件,并且使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
18.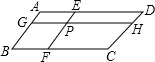 如图,在平行四边形ABCD中,过点P作直线EF、GH分别平行于AB、BC,那么图中共有( )平行四边形.
如图,在平行四边形ABCD中,过点P作直线EF、GH分别平行于AB、BC,那么图中共有( )平行四边形.
 如图,在平行四边形ABCD中,过点P作直线EF、GH分别平行于AB、BC,那么图中共有( )平行四边形.
如图,在平行四边形ABCD中,过点P作直线EF、GH分别平行于AB、BC,那么图中共有( )平行四边形.| A. | 4个 | B. | 5个 | C. | 8个 | D. | 9个 |
8.对于“$\sqrt{5}$”,有下列说法:①它是一个无理数;②它是数轴上离原点$\sqrt{5}$个单位长度的点所表示的数;③若$a<\sqrt{5}<a+1$,则整数a为2;④它表示面积为5的正方形的边长.其中正确说法的个数( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.已知甲、乙两数的和是6,甲数是乙数的3倍,设甲数为x,乙数为y,根据题意,列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=6}\\{x=3y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=6}\\{y=3x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+2y=6}\\{x=3y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=6}\\{y=3x}\end{array}\right.$ |
12. 如图,在?ABCD中,O是AC,BD的交点,过点O与AC垂直的直线交边AD于点E,若?ABCD的周长20厘米,则△CDE的周长为( )
如图,在?ABCD中,O是AC,BD的交点,过点O与AC垂直的直线交边AD于点E,若?ABCD的周长20厘米,则△CDE的周长为( )
 如图,在?ABCD中,O是AC,BD的交点,过点O与AC垂直的直线交边AD于点E,若?ABCD的周长20厘米,则△CDE的周长为( )
如图,在?ABCD中,O是AC,BD的交点,过点O与AC垂直的直线交边AD于点E,若?ABCD的周长20厘米,则△CDE的周长为( )| A. | 6厘米 | B. | 8厘米 | C. | 10厘米 | D. | 12厘米 |
13.下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(环) | 8.9 | 9.1 | 8.9 | 9.1 |
| 方差 | 3.3 | 3.8 | 3.8 | 3.3 |
| A. | 丁 | B. | 丙 | C. | 乙 | D. | 甲 |