题目内容
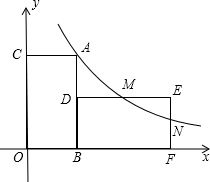 如图,面积为8的矩形ABOC的边OB,OC分别在x轴,y轴的正半轴上,点A在反比例函数y=
如图,面积为8的矩形ABOC的边OB,OC分别在x轴,y轴的正半轴上,点A在反比例函数y=| k |
| x |
(1)求反比例函数y=
| k |
| x |
(2)将矩形ABOC以点B为旋转中心,顺时针旋转90°后得到矩形BDEF,反比例函数图象交DE于M点,交EF于N点.求M,N的坐标;
(3)△MBN的面积.
考点:反比例函数综合题
专题:
分析:(1)根据矩形的面积,可得出矩形的长和宽,从而得出A点的坐标,代入曲线方程中即可得出k的值,便可得出反比例函数的解析式;
(2)结合题意,可得出点M的横坐标和点N的横坐标,由于点M和N均在曲线上,故可得出M和N的坐标;
(3)可得出EM的长和EN的长,在Rt△NME中,利用面积公式即可得出△MEN、△MDB、△NBF的面积,从而求得△MBN的面积.
(2)结合题意,可得出点M的横坐标和点N的横坐标,由于点M和N均在曲线上,故可得出M和N的坐标;
(3)可得出EM的长和EN的长,在Rt△NME中,利用面积公式即可得出△MEN、△MDB、△NBF的面积,从而求得△MBN的面积.
解答:解:(1)∵矩形ABOC的面积为8,AC=2,
∴AB=4,
∴点A的坐标为(2,4),
∵点A在双曲线y=
的图象上,所以4=
,
∴所求的双曲线的解析式为y=
;
(2)由题意可知点M的纵坐标为2,点N的横坐标为6,
∴M点的横坐标为4,N点的纵坐标为
,
∴点M的坐标为(4,2),N的坐标为(6,
);
(3)∵EM=2,EN=
,DM=2,
∴S△MEN=S矩形DGFE-△MDB-S△MEN-S△BFN=4×2-
[2×2+2×
+4×
]=
.
∴AB=4,
∴点A的坐标为(2,4),
∵点A在双曲线y=
| k |
| x |
| k |
| 2 |
∴所求的双曲线的解析式为y=
| 8 |
| x |
(2)由题意可知点M的纵坐标为2,点N的横坐标为6,
∴M点的横坐标为4,N点的纵坐标为
| 4 |
| 3 |
∴点M的坐标为(4,2),N的坐标为(6,
| 4 |
| 3 |
(3)∵EM=2,EN=
| 2 |
| 3 |
∴S△MEN=S矩形DGFE-△MDB-S△MEN-S△BFN=4×2-
| 1 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
点评:本题主要考查了反比例函数解析式的求法和矩形的性质以及三角形面积公式的应用,知识点较多,但不是太难,属于基础性题目.

练习册系列答案
相关题目
 如图所示,△ABC,AB=AC,EB=FC,BD=CE,∠A=52°,求∠DEF.
如图所示,△ABC,AB=AC,EB=FC,BD=CE,∠A=52°,求∠DEF. 如图所示,已知AB⊥BC,DC⊥BC,E在BC上,且AE=AD,AB=BC,求证:CE=CD.
如图所示,已知AB⊥BC,DC⊥BC,E在BC上,且AE=AD,AB=BC,求证:CE=CD. 在平面直角坐标系xOy中,抛物线y=x2-(m-1)x-m(m>0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
在平面直角坐标系xOy中,抛物线y=x2-(m-1)x-m(m>0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C. 如图,AB是⊙O的直径,且AD∥OC,若弧AD的度数为80°,求弧CD的度数.
如图,AB是⊙O的直径,且AD∥OC,若弧AD的度数为80°,求弧CD的度数.