题目内容
17．
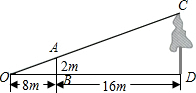如图，为了测量校园内某棵树的高度，张敏用长为2m的竹竿做测量工具，移动竹竿，使竹竿、树的顶端的影子恰好落在地面的同一点O处．此时，竹竿与O点相距8m，竹竿与树相距16m，则树的高度为6m．
分析 根据题意得出△AOB∽△COD，进而利用相似三角形的性质得出答案．
解答 解：由题意可得：AB∥DC，
则△AOB∽△COD，
故$\frac{AB}{DC}$=$\frac{BO}{DO}$，
则$\frac{2}{DC}$=$\frac{8}{24}$，
解得：DC=6，
故树的高度为6m．
故答案为：6．
点评 此题主要考查了相似三角形的应用，正确得出相似三角形是解题关键．
练习册系列答案
口算题天天练系列答案
相关题目
如图，将边长为6的等边△ABC放置在平面直角坐标系中，则A点坐标为（3，3$\sqrt{3}$）．
12．
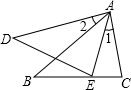如图，已知∠1=∠2，那么添加下列一个条件后，仍无法判定△ABC∽△ADE的是（ ）
如图，已知∠1=∠2，那么添加下列一个条件后，仍无法判定△ABC∽△ADE的是（ ）| A． | ∠C=∠AED | B． | $\frac{AB}{AD}=\frac{AC}{AE}$ | C． | ∠B=∠D | D． | $\frac{AB}{AD}=\frac{BC}{DE}$ |
2．
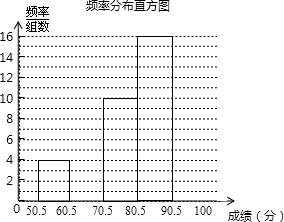6月5日是世界环保日．为了让学生了解环保知识，某中学组织全校2000名学生参加了“环保知识竞赛”．为了解本次竞赛成绩的分布情况，从中抽取了部分学生的成绩（满分100分，得分均为正整数）进行统计，得到下面的频率分布表和频数分布直方图．
请根据以上的统计图、表解答下列问题：
频率分布表
（1）补全频率分布表和频数分布直方图；
（2）被抽取的参赛学生中，竞赛成绩落在80.5-90.5分数段的人数最多；
（3）成绩在80分以上为良好，该校所有参赛学生中成绩良好的约为多少人？
6月5日是世界环保日．为了让学生了解环保知识，某中学组织全校2000名学生参加了“环保知识竞赛”．为了解本次竞赛成绩的分布情况，从中抽取了部分学生的成绩（满分100分，得分均为正整数）进行统计，得到下面的频率分布表和频数分布直方图．请根据以上的统计图、表解答下列问题：
频率分布表
| 分数段 | 频数 | 频率 |
| 50.5-60.5 | 4 | 0.08 |
| 60.5-70.5 | 8 | 0.16 |
| 70.5-80.5 | 10 | 0.20 |
| 80.5-90.5 | 16 | 0.32 |
| 90.5-100.5 | 12 | 0.24 |
| 合计 | 1 |
（2）被抽取的参赛学生中，竞赛成绩落在80.5-90.5分数段的人数最多；
（3）成绩在80分以上为良好，该校所有参赛学生中成绩良好的约为多少人？
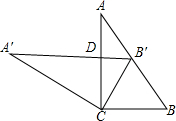如图，将两块大小相同的三角板重叠在一起，∠A=30°，∠B=60°，BC=10cm，把上面一块三角板绕顶点C作逆时针方向旋转到△A′B′C′的位置，点B′在AB上，A′B′与AC相交于点D，则A′D的长度为（ ）