题目内容
2.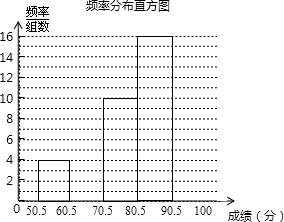 6月5日是世界环保日.为了让学生了解环保知识,某中学组织全校2000名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分100分,得分均为正整数)进行统计,得到下面的频率分布表和频数分布直方图.
6月5日是世界环保日.为了让学生了解环保知识,某中学组织全校2000名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分100分,得分均为正整数)进行统计,得到下面的频率分布表和频数分布直方图.请根据以上的统计图、表解答下列问题:
频率分布表
| 分数段 | 频数 | 频率 |
| 50.5-60.5 | 4 | 0.08 |
| 60.5-70.5 | 8 | 0.16 |
| 70.5-80.5 | 10 | 0.20 |
| 80.5-90.5 | 16 | 0.32 |
| 90.5-100.5 | 12 | 0.24 |
| 合计 | 1 |
(2)被抽取的参赛学生中,竞赛成绩落在80.5-90.5分数段的人数最多;
(3)成绩在80分以上为良好,该校所有参赛学生中成绩良好的约为多少人?
分析 (1)根据成绩在50.5-60.5的频数和频率计算出总人数,再根据频率=频数÷总数分别计算出80.5-90.5、90.5-100.5两区间的频数和频率,根据分布表补全直方图;
(2)根据频数分布直方图可知成绩落在80.5-90.5的人数最多;
(3)根据样本中良好人数所占比例可估计总体中达到良好的人数.
解答 解:(1)根据频率分布表可知,抽查的学生总数为:4÷0.08=50(人),
则成绩为80.5-90.5的人数为:0.32×50=16(人),
成绩在90.5-100.5的频率为:12÷50=0.24,
补全分布直方图如下:
(2)由频数分布直方图可知,成绩落在80.5-90.5的人数最多;
(3)该校所有参赛学生中成绩良好的约为:$\frac{16+12}{50}$×2000=1120(人),
故答案为:(1)16,0.24;(2)80.5-90.5.
点评 本题主要考查频率分布表和频数分布直方图及用样本估计总体,从表格中获取有用信息是解题关键,通晓统计中的计算公式是根本.

练习册系列答案
相关题目
12.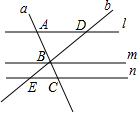 如图,已知直线l∥m∥n,直线a分别与l,m,n交于点A,B,C,过点B作直线b交直线l,n于点D,E,若AB=2,BC=1,BD=3,则BE的长为( )
如图,已知直线l∥m∥n,直线a分别与l,m,n交于点A,B,C,过点B作直线b交直线l,n于点D,E,若AB=2,BC=1,BD=3,则BE的长为( )
 如图,已知直线l∥m∥n,直线a分别与l,m,n交于点A,B,C,过点B作直线b交直线l,n于点D,E,若AB=2,BC=1,BD=3,则BE的长为( )
如图,已知直线l∥m∥n,直线a分别与l,m,n交于点A,B,C,过点B作直线b交直线l,n于点D,E,若AB=2,BC=1,BD=3,则BE的长为( )| A. | 4 | B. | 2 | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
10.下列分解因式结果正确的是( )
| A. | y3-y=y(y2-1) | B. | x2-x-3=x(x-1)-3 | C. | -m2+n2=-(m-n)(m+n) | D. | x2-3x+9=(x-3)2 |
7.下列计算正确的是( )
| A. | x2+x3=2x5 | B. | (-x3)2=-x6 | C. | x6÷x3=x3 | D. | x2•x3=x6 |
11.如图,经过折叠能围成一个正方体的是( )
| A. |  | B. |  | C. |  | D. |  |
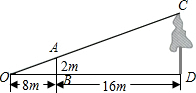 如图,为了测量校园内某棵树的高度,张敏用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点O处.此时,竹竿与O点相距8m,竹竿与树相距16m,则树的高度为6m.
如图,为了测量校园内某棵树的高度,张敏用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点O处.此时,竹竿与O点相距8m,竹竿与树相距16m,则树的高度为6m.
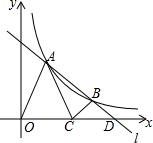 如图,直线l与双曲线$y=\frac{k}{x}$的一支相交于A、B两点,l与x轴相交于点D,C为线段OD中点,△OAC与△BCD分别是以OC、CD为底的等腰三角形,且S△OAC+S△BCD=2,则k=$\frac{3}{2}$.
如图,直线l与双曲线$y=\frac{k}{x}$的一支相交于A、B两点,l与x轴相交于点D,C为线段OD中点,△OAC与△BCD分别是以OC、CD为底的等腰三角形,且S△OAC+S△BCD=2,则k=$\frac{3}{2}$.