题目内容
12.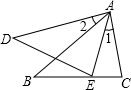 如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )| A. | ∠C=∠AED | B. | $\frac{AB}{AD}=\frac{AC}{AE}$ | C. | ∠B=∠D | D. | $\frac{AB}{AD}=\frac{BC}{DE}$ |
分析 先根据∠1=∠2得出∠BAC=∠DAE,再由相似三角形的判定定理对各选项进行逐一判定即可.
解答 解:∵∠1=∠2,
∴∠BAC=∠DAE.
A、∵∠C=∠AED,∴△ABC∽△ADE,故本选项错误;
B、∵$\frac{AB}{AD}$=$\frac{AC}{AE}$,∴△ABC∽△ADE,故本选项错误;
C、∵∠B=∠D,∴△ABC∽△ADE,故本选项错误;
D、∵$\frac{AB}{AD}$=$\frac{BC}{DE}$,∠B与∠D的大小无法判定,∴无法判定△ABC∽△ADE,故本选项正确.
故选D.
点评 本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
2. 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )
 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
3.下列说法中正确的是( )
| A. | 0不是有理数 | B. | 有理数不是整数就是分数 | ||
| C. | 在有理数中有最小的数 | D. | a是有理数,则-a一定是负数 |
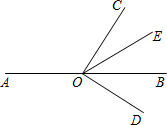 如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC.
如图,O是直线AB上一点,∠COD是直角,OE平分∠BOC.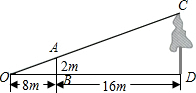 如图,为了测量校园内某棵树的高度,张敏用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点O处.此时,竹竿与O点相距8m,竹竿与树相距16m,则树的高度为6m.
如图,为了测量校园内某棵树的高度,张敏用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点O处.此时,竹竿与O点相距8m,竹竿与树相距16m,则树的高度为6m.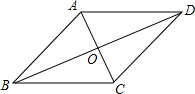 如图,平行四边形ABCD中,对角线AC、BD相交于点O,现从以下四个式子①AB=BC,②AC=BD,③AC⊥BD,④∠ABC=90°中,任取一个作为条件,即可推出平行四边形ABCD是菱形的概率为$\frac{1}{2}$.
如图,平行四边形ABCD中,对角线AC、BD相交于点O,现从以下四个式子①AB=BC,②AC=BD,③AC⊥BD,④∠ABC=90°中,任取一个作为条件,即可推出平行四边形ABCD是菱形的概率为$\frac{1}{2}$.