题目内容
6. 如图,矩形ABCD中,E是BC上一点,且$\frac{BE}{EC}$=4,AE⊥DE,求$\frac{AB}{BC}$的值.
如图,矩形ABCD中,E是BC上一点,且$\frac{BE}{EC}$=4,AE⊥DE,求$\frac{AB}{BC}$的值.
分析 根据题意可得出△ABE∽△ECD,则 $\frac{AB}{EC}$=$\frac{BE}{CD}$,设BE=x,则EC=4x,从而得出AB=CD=2x,再求比值即可.
解答 解:∵∠B=∠C=90°,
∴∠BAE+∠AEB=90°,
∵AE⊥DE,
∴∠AEB+∠CED=90°,
∴∠BAE=∠CED,
∴△ABE∽△ECD,
∴$\frac{AB}{EC}$=$\frac{BE}{CD}$,
设BE=x,
∵BE:EC=1:4,
∴EC=4x,
∴AB•CD=x•4x,
∴AB=CD=2x,
∴AB:BC=2x:5x=2:5.
故答案为2:5.
点评 本题考查了相似三角形的判定和性质/矩形的性质等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.若点P(a,b)在第四象限内,则Q(b,-a)所在象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.下列结论中,正确的是( )
| A. | 把一个角分成两个角的射线叫角平分线 | |
| B. | 两点确定一条直线 | |
| C. | 若AB=BC,则点B是线段AC的中点 | |
| D. | 两点之间,直线最短 |
18.方程x2=9的解是( )
| A. | x=9 | B. | x=±9 | C. | x=3 | D. | x=±3 |
15. 如图,AB∥CD,CD⊥EF,若∠1=124°,则∠2=( )
如图,AB∥CD,CD⊥EF,若∠1=124°,则∠2=( )
 如图,AB∥CD,CD⊥EF,若∠1=124°,则∠2=( )
如图,AB∥CD,CD⊥EF,若∠1=124°,则∠2=( )| A. | 56° | B. | 66° | C. | 24° | D. | 34° |
16.下列调查中,调查方式选择不合理的是( )
| A. | 了解某电视台某次“爱的奉献”抗震救灾文艺晚会的收视率,采用抽样调查的方式 | |
| B. | 了解某渔场中青鱼的平均重量,采用抽样调查 | |
| C. | 了解某型号联想电脑的使用寿命,采用全面调查 | |
| D. | 了解一批汽车的刹车性能,采用全面调查 |
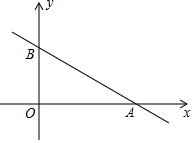 如图,在平面直角坐标系内A(8,0),B(0,6),若直线L与AB平行,且在直线L上有且只有一点P使∠OPA=90°,求满足条件的直线L的解析式.
如图,在平面直角坐标系内A(8,0),B(0,6),若直线L与AB平行,且在直线L上有且只有一点P使∠OPA=90°,求满足条件的直线L的解析式.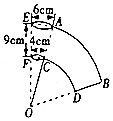 如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4cm,母线长EF=9cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π)
如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4cm,母线长EF=9cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π)