题目内容
8.若正比例函数y=kx(k≠0)的图象经过点P(-2,3),则该函数的图象经过的点是( )| A. | (3,-2) | B. | (1,-6) | C. | (2,-3) | D. | (-1,-6) |
分析 先把点P(-2,3)代入正比例函数y=kx(k≠0),求出k的值,故可得出此函数的解析式,再把各点代入此函数的解析式进行检验即可.
解答 解:∵正比例函数y=kx(k≠0)的图象经过点P(-2,3),
∴3=-2k,解得k=-$\frac{3}{2}$,
∴正比例函数的解析式为y=-$\frac{3}{2}$x.
A、∵当x=3时,y=-$\frac{9}{2}$≠-2,∴此点不在正比例函数的图象上,故本选项错误;
B、∵当x=1时,y=-$\frac{3}{2}$≠-6,∴此点不在正比例函数的图象上,故本选项错误;
C、当x=2时,y=-3,∴此点在正比例函数的图象上,故本选项正确;
D、当x=-1时,y=$\frac{3}{2}$≠-6,∴此点不在正比例函数的图象上,故本选项错误.
故选C.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
16.在某次数学摸底考试中有3个男同学和2个女同学获得了满分,要想从中随机挑选一个同学参加市数学竞赛,其中选中男生的概率是( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | 1 |
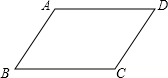 已知:如图,四边形ABCD是平行四边形.
已知:如图,四边形ABCD是平行四边形.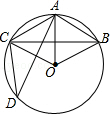 如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°.
如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°.