题目内容
1. 如图是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为110.
如图是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为110.
分析 延长AB交KF于点O,延长AC交GM于点P,可得四边形AOLP是正方形,然后求出正方形的边长,再求出矩形KLMJ的长与宽,然后根据矩形的面积公式列式计算即可得解.
解答 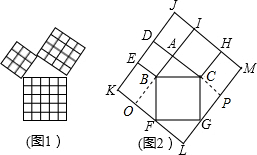 解:如图,延长AB交KF于点O,延长AC交GM于点P,则四边形OALP是矩形.
解:如图,延长AB交KF于点O,延长AC交GM于点P,则四边形OALP是矩形.
∵∠CBF=90°,
∴∠ABC+∠OBF=90°,
又∵直角△ABC中,∠ABC+∠ACB=90°,
∴∠OBF=∠ACB,
在△OBF和△ACB中,
$\left\{\begin{array}{l}{∠BAC=∠BOF}\\{∠ACB=∠OBF}\\{BC=BF}\end{array}\right.$,
∴△OBF≌△ACB(AAS),
∴AC=OB,
同理:△ACB≌△PGC,
∴PC=AB,
∴OA=AP,
所以,矩形AOLP是正方形,
边长AO=AB+AC=3+4=7,
所以,KL=3+7=10,LM=4+7=11,
因此,矩形KLMJ的面积为10×11=110.
故答案是:110.
点评 本题考查了勾股定理的证明,作出辅助线构造出正方形是解题的关键.

练习册系列答案
相关题目
11.三元一次方程组$\left\{\begin{array}{l}{5x+4y+z=0}\\{3x+y-4z=11}\\{x+y+z=-2}\end{array}\right.$,消去未知数z后,得到的二元一次方程组是( )
| A. | $\left\{\begin{array}{l}{4x+3y=2}\\{7x+5y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{4x+3y=2}\\{23x+17y=11}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{3x+4y=2}\\{7x+5y=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x+4y=2}\\{23x+17y=11}\end{array}\right.$ |
12.下列四组条件中,能识别△ABC与△DEF相似的是( )
| A. | ∠A=45°,∠B=55°;∠D=45°∠F=75° | |
| B. | AB=5,BC=4,∠A=45°;DE=10,EF=8,∠D=45° | |
| C. | AB=6,BC=5,∠B=40°;DE=5,EF=6,∠E=40° | |
| D. | BC=4,AC=6,AB=9;DE=6,EF=12,DF=18 |
10.如果一个三角形的三个外角的度数之比是2:3:4,那么与之对应的三个内角的度数之比是( )
| A. | 1:3:5 | B. | 2:3:4 | C. | 4:3:2 | D. | 5:3:1 |