题目内容
8．
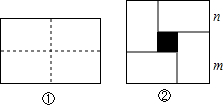图①是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图②的形状拼成一个正方形．（1）将图②中的阴影部分面积用2种方法表示可得一个等式，这个等式为（m+n）2-4mn=（m-n）2．
（2）若m+2n=7，mn=3，利用（1）的结论求m-2n的值．
分析 （1）大正方形的面积减去矩形的面积即可得出阴影部分的面积，也可得出三个代数式（m+n）2、（m-n）2、mn之间的等量关系；
（2）根据（1）所得出的关系式，可求出（m-2n）2，继而可得出m-2n的值．
解答 解：（1）（m+n）2-4mn=（m-n）2；故答案为：（m+n）2-4mn=（m-n）2
（2）（m-2n）2=（m+2n）2-8mn=25，
则m-2n=±5．
点评 本题考查了完全平方公式的几何背景，属于基础题，注意仔细观察图形，表示出各图形的面积是关键．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
18．在实数：3.1415926，$\sqrt{2}$，1.010010001（每两个1之间依次多一个0），3.$\stackrel{••}{15}$，$\frac{22}{7}$中，无理数的个数为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
3．为了鼓励市民节约用水，某市居民生活用水按阶梯式水价计费．下表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息：
（说明：①每户产生的污水量等于该户的用水量，②水费=自来水费+污水处理费）已知小明家2014年4月份用水20吨，交水费66元；5月份用水35吨，交水费150元．
（1）求a、b的值．
（2）实行“阶梯水价”收费之后，该市一户居民6月用水27吨，其当月交水费多少元？
| 用户每月用水量 | 自来水单价（元/吨） | 污水处理费用（元/吨） |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
（1）求a、b的值．
（2）实行“阶梯水价”收费之后，该市一户居民6月用水27吨，其当月交水费多少元？
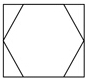将一个边长为1的正六边形补成如图所示的矩形，则矩形的周长等于4+2$\sqrt{3}$．（结果保留根号）
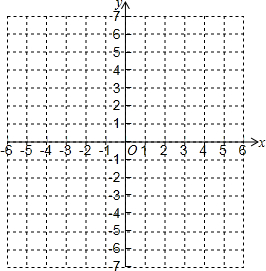如图所示的直角坐标系中，三角形ABC的顶点A坐标是（-3，0）、B点的坐标是（5，0）、点C在二四象限的夹角平分线上，已知三角形ABC的面积=24．求出点C的坐标；并画出图形．
18．比例尺为1：1000的图纸上某区域面积400cm2，则实际面积为（ ）
| A． | 4×105m2 | B． | 4×104m2 | C． | 1.6×105m2 | D． | 2×104m2 |