题目内容
17．
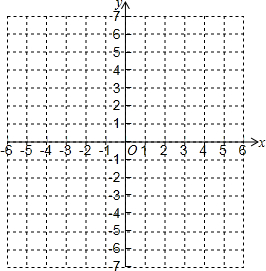如图所示的直角坐标系中，三角形ABC的顶点A坐标是（-3，0）、B点的坐标是（5，0）、点C在二四象限的夹角平分线上，已知三角形ABC的面积=24．求出点C的坐标；并画出图形．
分析 由点C在第二、四象限的夹角平分线上，设：点C的坐标为（a，-a），由三角形的面积即可求得．
解答 
解：∵点C在第二、四象限的夹角平分线上，
∴设：点C的坐标为（a，-a），
∵点A坐标是（-3，0）、B点的坐标是（5，0），
∴AB=8，
∴S△ABC=$\frac{1}{2}$×8×|-a|=24，
∴a=±6，
∴C（6，-6），（-6，6）；
如图所示：
点评 本题考查了基本作图，三角形的面积公式，角平分线的性质，掌握基本作图的方法是解题的关键．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
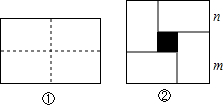图①是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图②的形状拼成一个正方形．
5．计算：8-1=（ ）
| A． | $\frac{1}{8}$ | B． | -8 | C． | 8 | D． | 不能确定 |