题目内容
16．O是△ABC的内心，∠A=70°，则∠BOC=125°．分析 利用三角形的内心的性质得出∠ABO+∠ACO=∠OBC+∠OCB=65°，进而得出答案．
解答 解：∵点O是△ABC的内心，
∴∠ABO=∠OBC，∠ACO=∠OCB，
∵∠A=70°，
∴∠ABC+∠ACB=110°，
∴∠ABO+∠ACO=∠OBC+∠OCB=55°，
则∠BOC=180°-55°=125°，
故答案为：125°．
点评 本题主要考查了三角形内心的性质以及三角形内角和定理，根据已知得出∠ABO+∠ACO=∠OBC+∠OCB是解题关键．
练习册系列答案
相关题目
4．若关于x的一元二次方程（k-1）x2+2x-2=0有实数根，则k的取值范围是（ ）
| A． | k＞$\frac{1}{2}$ | B． | k≥$\frac{1}{2}$ | C． | k＞$\frac{1}{2}$且k≠1 | D． | k≥$\frac{1}{2}$且k≠1 |
11．下列计算正确的是（ ）
| A． | （-2）2=-2 | B． | a2+a3=a | C． | （3a2）2=3a4 | D． | x6÷x2=x4 |
如图，在△ABC中，以AC为直径作⊙O交BC于D点，交AB于G点，且D是BC的中点，DE⊥AB于E点，交AC的延长线于点F．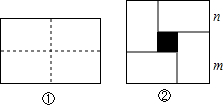
图①是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图②的形状拼成一个正方形．
5．计算：8-1=（ ）
| A． | $\frac{1}{8}$ | B． | -8 | C． | 8 | D． | 不能确定 |