题目内容
8. 如图,矩形ABCD中,AB:BC=$\sqrt{2}$:1,把矩形ABCD沿EF对折,请你判断矩形AEFD与矩形ABCD相似吗?为什么?
如图,矩形ABCD中,AB:BC=$\sqrt{2}$:1,把矩形ABCD沿EF对折,请你判断矩形AEFD与矩形ABCD相似吗?为什么?
分析 设BC=x,根据题意表示出两个矩形的各边,计算对应边的比,根据相似多边形的判定定理进行证明即可.
解答 解:设BC=x,则AB=$\sqrt{2}$x,DF=$\frac{\sqrt{2}}{2}$x,
$\frac{DF}{AD}$=$\frac{\sqrt{2}}{2}$,$\frac{AD}{AB}$=$\frac{x}{\sqrt{2}x}$=$\frac{\sqrt{2}}{2}$,
由矩形的四个角都是90°,
则矩形AEFD与矩形ABCD相似.
点评 本题考查的是相似多边形的判定,掌握对应角相等、对应边的比相等的多边形相似是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
13.若|a|=2,|b|=3,且a>b,则a+b=( )
| A. | -1 | B. | -5 | C. | -1或-5 | D. | 以上答案都不对 |
20.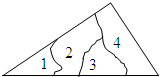 如图,小明把一块三角形的玻璃打碎成了四块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法( )
如图,小明把一块三角形的玻璃打碎成了四块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法( )
 如图,小明把一块三角形的玻璃打碎成了四块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法( )
如图,小明把一块三角形的玻璃打碎成了四块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法( )| A. | 选①去 | B. | 选②去 | C. | 选③去 | D. | 选④去 |
17. 如图中的俯视图是( )
如图中的俯视图是( )
 如图中的俯视图是( )
如图中的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
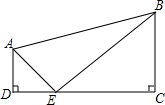 如图,在四边形ABCD中,AD∥BC,∠C=∠D=90°,AD=2,BC=3,CD=7,若点E是边DC上的一个动点,当DE为何值时,△EAD与△EBC相似?
如图,在四边形ABCD中,AD∥BC,∠C=∠D=90°,AD=2,BC=3,CD=7,若点E是边DC上的一个动点,当DE为何值时,△EAD与△EBC相似?