题目内容
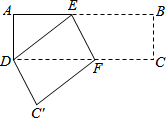 在长方形纸片ABCD中,AD=3cm,AB=9cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=
在长方形纸片ABCD中,AD=3cm,AB=9cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=考点:翻折变换(折叠问题)
专题:
分析:首先根据题意结合图形得到DE=BE;通过△EOB≌△FOD得到DF=BE;运用勾股定理求出DE的长度问题即可解决.
解答: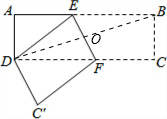 解:如图,连接BD,交EF于点O;
解:如图,连接BD,交EF于点O;
由题意得:DE=BE(设为x),DO=BO;
∵四边形ABCD为矩形,
∴BE∥DF,
∴∠EBO=∠FDO;
在△EOB与△FOD中,
,
∴△EOB≌△FOD(ASA),
∴DF=BE=x;
(1)∵AB=9,DE=BE=x,
∴AE=9-x;
根据勾股定理:
DE2=AD2+AE2,
∴x2=32+(9-x)2,
解得:x=5(cm),
(2)∵DF=5,AD=3,
∴S△DEF=
DF•AD=
×5×3=7.5(cm2);
即△DEF的面积是7.5;
故答案为:5;7.5.
 解:如图,连接BD,交EF于点O;
解:如图,连接BD,交EF于点O;由题意得:DE=BE(设为x),DO=BO;
∵四边形ABCD为矩形,
∴BE∥DF,
∴∠EBO=∠FDO;
在△EOB与△FOD中,
|
∴△EOB≌△FOD(ASA),
∴DF=BE=x;
(1)∵AB=9,DE=BE=x,
∴AE=9-x;
根据勾股定理:
DE2=AD2+AE2,
∴x2=32+(9-x)2,
解得:x=5(cm),
(2)∵DF=5,AD=3,
∴S△DEF=
| 1 |
| 2 |
| 1 |
| 2 |
即△DEF的面积是7.5;
故答案为:5;7.5.
点评:该命题以矩形为载体,以图形的翻折变换为手段,以考查勾股定理、折叠的性质及其应用为核心构造而成;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
数轴上表示-9与9的两个点之间的距离是( )
| A、0 | B、18 | C、9 | D、无法计算 |
 如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有
如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有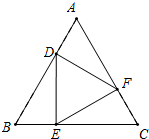 如图,在边长为3的等边△ABC中,D、E、F分别是AB、BC、AC上的点,AD=BE=CF=1.
如图,在边长为3的等边△ABC中,D、E、F分别是AB、BC、AC上的点,AD=BE=CF=1.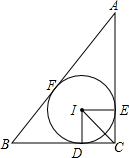 如图,在△ABC中,∠C=90°,内切圆⊙I与AC、BC分别相切于点E,D.
如图,在△ABC中,∠C=90°,内切圆⊙I与AC、BC分别相切于点E,D. 如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,
如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,