题目内容
已知ab=4,若2≥b≥1,则a的取值范围是________.
 4≥a≥2
【解析】根据已知条件可以求得b=,然后将b的值代入不等式2≥b≥1,通过解该不等式即可求得a的取值范围4≥a≥2.
故答案为:4≥a≥2.
4≥a≥2
【解析】根据已知条件可以求得b=,然后将b的值代入不等式2≥b≥1,通过解该不等式即可求得a的取值范围4≥a≥2.
故答案为:4≥a≥2.
 通城学典默写能手系列答案
通城学典默写能手系列答案阅读下列材料:
解答“已知 ,试确定
,试确定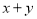 的取值范围”有如下解法:
的取值范围”有如下解法:
【解析】
∵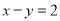 ,∴x=y+2,又∵
,∴x=y+2,又∵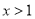 ,∴
,∴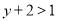 ,即
,即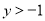
又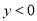 ,∴
,∴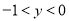 .…①
.…①
同理得: 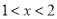 .…②
.…②
由①+②得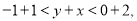
∴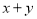 的取值范围是
的取值范围是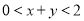 .
.
请按照上述方法,完成下列问题 :
已知关于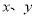 的方程组
的方程组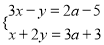 的解都是正数.
的解都是正数.
(1)求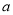 的取值范围;
的取值范围;
(2)已知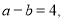 且
且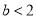 ,求
,求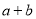 的取值范围;
的取值范围;
(3) 已知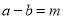 (
(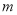 是大于0的常数),且
是大于0的常数),且 的最大值.(用
的最大值.(用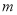 含的式子表示)
含的式子表示)
 (1);(2)(3)
【解析】(1 ) x=a-1, y=a+2(2分) (3分)
(2) 1
(1);(2)(3)
【解析】(1 ) x=a-1, y=a+2(2分) (3分)
(2) 1如图所示,在 ABCD中,E,F,G,H分别是四条边上的点,且满足AE=CF,BG=DH,连接EF,GH.试说明EF和GH互相平分.
ABCD中,E,F,G,H分别是四条边上的点,且满足AE=CF,BG=DH,连接EF,GH.试说明EF和GH互相平分.
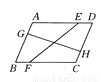
 答案见解析
【解析】试题分析:如图,连接EG,GF,FH,HE,证明四边形EGFH是平行四边形,问题即可解决.
试题解析:【解析】
连接EG,GF,FH,HE.如图,∵四边形ABCD为平行四边形,∴∠B=∠D,AD=BC.又∵AE=CF,∴AD-AE=BC-CF,即DE=BF.又∵DH=BG,∴△BFG≌△DEH(SAS),∴GF=EH,同理GE=FH,∴四边形EGFH平行四边形,∴...
答案见解析
【解析】试题分析:如图,连接EG,GF,FH,HE,证明四边形EGFH是平行四边形,问题即可解决.
试题解析:【解析】
连接EG,GF,FH,HE.如图,∵四边形ABCD为平行四边形,∴∠B=∠D,AD=BC.又∵AE=CF,∴AD-AE=BC-CF,即DE=BF.又∵DH=BG,∴△BFG≌△DEH(SAS),∴GF=EH,同理GE=FH,∴四边形EGFH平行四边形,∴... 下列条件中,能判别四边形是平行四边形的是 ( )
A. 一组对边相等,另一组对边平行 B. 一组对边平行,一组对角互补
C. 一组对角相等,一组邻角互补 D. 一组对角互补,另一组对角相等
 C
【解析】解:A.一组对边相等,另一组对边平行,也有可能是等腰梯形;
B.一组对边平行,一组对角互补,也有可能是等腰梯形;
C.一组对角相等,一组邻角互补可得到两组对角分别相等,所以是平行四边形;
D.一组对角互补,另一组对角相等,可能是含两个直角的一般四边形.
故选C.
C
【解析】解:A.一组对边相等,另一组对边平行,也有可能是等腰梯形;
B.一组对边平行,一组对角互补,也有可能是等腰梯形;
C.一组对角相等,一组邻角互补可得到两组对角分别相等,所以是平行四边形;
D.一组对角互补,另一组对角相等,可能是含两个直角的一般四边形.
故选C. 在实数范围内定义一种新运算“⊕”,其运算规则为:a⊕b=-2a+3b.如:1⊕5=-2×1+3×5=13.则不等式x⊕4<0的解集为____.
 4
【解析】试题解析:x?4=2x+3×4=0
解得:x=6.
4
【解析】试题解析:x?4=2x+3×4=0
解得:x=6. 下列各式中,是一元一次不等式的是( )
A. 5+4>8 B. 2x-1 C. 2x≤5 D.
D. 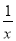 -3x≥0
-3x≥0
 C
【解析】试题解析:A、是不等式,但不是一元一次不等式,故本选项错误;
B、是一元一次方程,不是一元一次不等式,故本选项错误;
C、是一元一次不等式,故本选项正确;
D、不是一元一次不等式,故本选项错误;
故选C.
C
【解析】试题解析:A、是不等式,但不是一元一次不等式,故本选项错误;
B、是一元一次方程,不是一元一次不等式,故本选项错误;
C、是一元一次不等式,故本选项正确;
D、不是一元一次不等式,故本选项错误;
故选C. 我们知道过n边形的一个顶点可以做(n-3)条对角线,这(n-3)条对角线把三角形分割成(n-2)个三角形,想一想这是为什么?如图1.
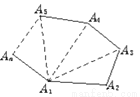
图1
如图2,在n边形的边上任意取一点,连结这点与各顶点的线段可以把n边形分成几个三角形?
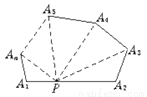
图2
想一想,利用这两个图形,怎样证明多边形的内角和定理.
 n-2.想一想见解析
【解析】分析:本题主要考查利用三角形内角和定理来证明多边形的内角和定理,从多边形的一个顶点出发引对角线,则把n边形分成(n-2)个三角形从而证明多边形的内角和定理.
本题解析:
(1)因为对角线是连结不相邻的两个顶点之间的线段,每一个顶点都有两个相邻的顶点,所以有(n-3)条对角线,三条边组成一个三角形,(1)图可分成(n-2)个三角形,
(2)图可分...
n-2.想一想见解析
【解析】分析:本题主要考查利用三角形内角和定理来证明多边形的内角和定理,从多边形的一个顶点出发引对角线,则把n边形分成(n-2)个三角形从而证明多边形的内角和定理.
本题解析:
(1)因为对角线是连结不相邻的两个顶点之间的线段,每一个顶点都有两个相邻的顶点,所以有(n-3)条对角线,三条边组成一个三角形,(1)图可分成(n-2)个三角形,
(2)图可分... 如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
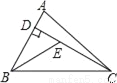
A. 10 B. 7 C. 5 D. 4
 C
【解析】作EF⊥BC于F,
∵BE平分∠ABC,ED⊥AB,EF⊥BC,
∴EF=DE=2,
∴S△BCE=BC?EF=×5×2=5,
故选C.
C
【解析】作EF⊥BC于F,
∵BE平分∠ABC,ED⊥AB,EF⊥BC,
∴EF=DE=2,
∴S△BCE=BC?EF=×5×2=5,
故选C. 如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为__cm.
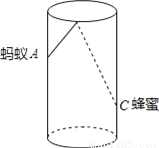
 5
【解析】试题分析:沿过A的圆柱的高剪开,得出矩形EFGH,过C作CQ⊥EF于Q,作A关于EH的对称点,连接交EH于P,连接AP,
则AP+PC就是蚂蚁到达蜂蜜的最短距离,∵AE= , =AP,∴AP+PC= +PC= ,∵CQ=×18=9cm, =12-4+4=12cm,在Rt△中,由勾股定理得: ==15cm.故答案为15.
5
【解析】试题分析:沿过A的圆柱的高剪开,得出矩形EFGH,过C作CQ⊥EF于Q,作A关于EH的对称点,连接交EH于P,连接AP,
则AP+PC就是蚂蚁到达蜂蜜的最短距离,∵AE= , =AP,∴AP+PC= +PC= ,∵CQ=×18=9cm, =12-4+4=12cm,在Rt△中,由勾股定理得: ==15cm.故答案为15. 
