题目内容
阅读下列材料:
解答“已知 ,试确定
,试确定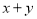 的取值范围”有如下解法:
的取值范围”有如下解法:
【解析】
∵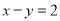 ,∴x=y+2,又∵
,∴x=y+2,又∵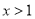 ,∴
,∴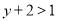 ,即
,即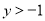
又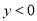 ,∴
,∴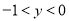 .…①
.…①
同理得: 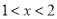 .…②
.…②
由①+②得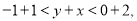
∴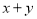 的取值范围是
的取值范围是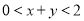 .
.
请按照上述方法,完成下列问题 :
已知关于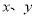 的方程组
的方程组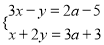 的解都是正数.
的解都是正数.
(1)求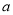 的取值范围;
的取值范围;
(2)已知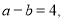 且
且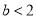 ,求
,求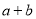 的取值范围;
的取值范围;
(3) 已知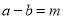 (
(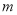 是大于0的常数),且
是大于0的常数),且 的最大值.(用
的最大值.(用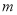 含的式子表示)
含的式子表示)
 (1);(2)(3)
【解析】(1 ) x=a-1, y=a+2(2分) (3分)
(2) 1
(1);(2)(3)
【解析】(1 ) x=a-1, y=a+2(2分) (3分)
(2) 1
练习册系列答案
相关题目
四条线段的长分别是5cm,6cm,8cm,13cm,以其中任意三条线段为边可以构成______个三角形.
 2
【解析】首先发现每三条可以组合为5、6、8;5、6、13;5、8、13;6、8、13;
再根据三角形的三边关系,可知能构成三角形的为:5、6、8和6、8、13.
因此可构成2个三角形.
故答案为:2.
2
【解析】首先发现每三条可以组合为5、6、8;5、6、13;5、8、13;6、8、13;
再根据三角形的三边关系,可知能构成三角形的为:5、6、8和6、8、13.
因此可构成2个三角形.
故答案为:2. 已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )

A. -1<x<4 B. -1<x<3 C. x<-1或x>4 D. x<-1或x>3
 B
【解析】由图象知,抛物线与x轴交于(-1,0),对称轴为x=1,
∴抛物线与x轴的另一交点坐标为(3,0),
∵y<0时,函数的图象位于x轴的下方,
且当-1<x<3时函数图象位于x轴的下方,
∴当-1<x<3时,y<0.
故选B.
B
【解析】由图象知,抛物线与x轴交于(-1,0),对称轴为x=1,
∴抛物线与x轴的另一交点坐标为(3,0),
∵y<0时,函数的图象位于x轴的下方,
且当-1<x<3时函数图象位于x轴的下方,
∴当-1<x<3时,y<0.
故选B. 二次函数y=x2-4x-3的顶点坐标是_____________.
 (2,﹣7)
【解析】试题分析:原式化为顶点式解析式,即为y=(x-2)2-7,所以其顶点坐标是(2,﹣7).
(2,﹣7)
【解析】试题分析:原式化为顶点式解析式,即为y=(x-2)2-7,所以其顶点坐标是(2,﹣7). 如图,若a<0,b>0,c<0,则抛物线y=ax2+bx+c的大致图象为( )
A. 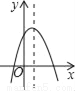 B.
B. 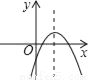 C.
C. 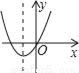 D.
D. 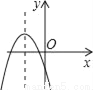
 B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B.
B
【解析】试题分析:∵a<0,
∴抛物线的开口方向向下,
故第三个选项错误;
∵c<0,
∴抛物线与y轴的交点为在y轴的负半轴上,
故第一个选项错误;
∵a<0、b>0,对称轴为x=>0,
∴对称轴在y轴右侧,
故第四个选项错误.
故选B. 任取不等式组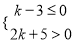 的一个整数解,则能使关于x的方程:2x+k=-1的解为非负数的可能性为____.
的一个整数解,则能使关于x的方程:2x+k=-1的解为非负数的可能性为____.
 【解析】解不等式k-3≤0可得k≤3,解不等式2k+5>0,可得k>-,所以可求得不等式组的解集为-<k≤3,所以k的整数解为-2、-1、0、1、2、3,分别代入方程2x+k=-1,可得x=、0、-、-1、-、-2,所以非负数解有了两个,其可能性为: .
故答案为: .
【解析】解不等式k-3≤0可得k≤3,解不等式2k+5>0,可得k>-,所以可求得不等式组的解集为-<k≤3,所以k的整数解为-2、-1、0、1、2、3,分别代入方程2x+k=-1,可得x=、0、-、-1、-、-2,所以非负数解有了两个,其可能性为: .
故答案为: . 不等式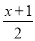 >
> -1的正整数解的个数是( )
-1的正整数解的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
 D
【解析】根据不等式的解法,去分母,得3(x+1)>2(2x+2)-6,去括号得3x+3>4x+4-6,移项合并同类项,x<5,可得其正整数解为1、2、3、4,共4个.
故选:D.
D
【解析】根据不等式的解法,去分母,得3(x+1)>2(2x+2)-6,去括号得3x+3>4x+4-6,移项合并同类项,x<5,可得其正整数解为1、2、3、4,共4个.
故选:D. 下列不能作为判定四边形ABCD为平行四边形的条件的是( )
A. AB=CD,AD=BC B. AB CD
CD
C. AB=CD,AD∥BC D. AB∥CD,AD∥BC
 C
【解析】解:A.∵AB=CD,AD=BC,∴四边形ABCD的两组对边相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
B.∵AB∥CD,AB=CD,∴四边形ABCD的一组对边平行且相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
C.∵AB=CD,AD∥CD,无法判定四边形ABCD是平行四边形;故本选项合题意;
D.∵AB∥CD,AD∥BC,四边...
C
【解析】解:A.∵AB=CD,AD=BC,∴四边形ABCD的两组对边相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
B.∵AB∥CD,AB=CD,∴四边形ABCD的一组对边平行且相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
C.∵AB=CD,AD∥CD,无法判定四边形ABCD是平行四边形;故本选项合题意;
D.∵AB∥CD,AD∥BC,四边... 已知ab=4,若2≥b≥1,则a的取值范围是________.
 4≥a≥2
【解析】根据已知条件可以求得b=,然后将b的值代入不等式2≥b≥1,通过解该不等式即可求得a的取值范围4≥a≥2.
故答案为:4≥a≥2.
4≥a≥2
【解析】根据已知条件可以求得b=,然后将b的值代入不等式2≥b≥1,通过解该不等式即可求得a的取值范围4≥a≥2.
故答案为:4≥a≥2. 
