��Ŀ����
����֪����n���ε�һ�������������n��3�����Խ��ߣ��⣨n��3�����Խ��߰������ηָ�ɣ�n��2���������Σ���һ������Ϊʲô����ͼ1��
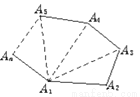
ͼ1
��ͼ2����n���εı�������ȡһ�㣬����������������߶ο���n���ηֳɼ��������Σ�
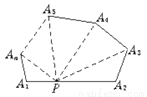
ͼ2
��һ�룬����������ͼ�Σ�����֤������ε��ڽǺͶ�����
 n-2����һ�������
��������������������Ҫ���������������ڽǺͶ�����֤������ε��ڽǺͶ������Ӷ���ε�һ������������Խ��ߣ����n���ηֳɣ�n-2)�������δӶ�֤������ε��ڽǺͶ���.
���������
(1)��Ϊ�Խ�����������ڵ���������֮����߶Σ�ÿһ�����㶼���������ڵĶ��㣬�����У�n-3)���Խ��ߣ����������һ�������Σ�(1)ͼ�ɷֳ�(n-2)��������,
(2)ͼ�ɷ�...
n-2����һ�������
��������������������Ҫ���������������ڽǺͶ�����֤������ε��ڽǺͶ������Ӷ���ε�һ������������Խ��ߣ����n���ηֳɣ�n-2)�������δӶ�֤������ε��ڽǺͶ���.
���������
(1)��Ϊ�Խ�����������ڵ���������֮����߶Σ�ÿһ�����㶼���������ڵĶ��㣬�����У�n-3)���Խ��ߣ����������һ�������Σ�(1)ͼ�ɷֳ�(n-2)��������,
(2)ͼ�ɷ�...
 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�����ʽ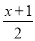 ��
�� ��1����������ĸ�����( )
��1����������ĸ�����( )
A. 1�� B. 2�� C. 3�� D. 4��
 D
�����������ݲ���ʽ�Ľⷨ��ȥ��ĸ����3��x+1����2��2x+2��-6��ȥ���ŵ�3x+3��4x+4-6������ϲ�ͬ���x��5���ɵ�����������Ϊ1��2��3��4����4��.
��ѡ��D.
D
�����������ݲ���ʽ�Ľⷨ��ȥ��ĸ����3��x+1����2��2x+2��-6��ȥ���ŵ�3x+3��4x+4-6������ϲ�ͬ���x��5���ɵ�����������Ϊ1��2��3��4����4��.
��ѡ��D. һ���ı��ε������ڽǵĶ����������£���ô������ƽ���ı��ε��ǣ� ��
A. 88�㣬108�㣬88�� B. 88�㣬104�㣬88��
C. 88�㣬92�㣬92�� D. 88�㣬92�㣬88��
 D
���������������ڽǶ���������88�㣬108�㣬88��ʱ,���ĸ�����76�㣬��A���ǣ�
����ԽǷֱ���ȵ��ı�����ƽ���ı��Σ���B���ǣ�
�������ڽǶ���������88�㣬92�㣬92��ʱ�����ĸ�����88�㣬��C����ȵ������Dz��ǶԽǹ�C����
D����������ԽǷֱ���ȣ������ƽ���ı��Ρ�
��ѡ��D.
D
���������������ڽǶ���������88�㣬108�㣬88��ʱ,���ĸ�����76�㣬��A���ǣ�
����ԽǷֱ���ȵ��ı�����ƽ���ı��Σ���B���ǣ�
�������ڽǶ���������88�㣬92�㣬92��ʱ�����ĸ�����88�㣬��C����ȵ������Dz��ǶԽǹ�C����
D����������ԽǷֱ���ȣ������ƽ���ı��Ρ�
��ѡ��D. ��֪ab��4����2��b��1����a��ȡֵ��Χ��________.
 4��a��2
��������������֪�����������b=��Ȼ��b��ֵ���벻��ʽ2��b��1��ͨ����ò���ʽ�������a��ȡֵ��Χ4��a��2��
�ʴ�Ϊ��4��a��2.
4��a��2
��������������֪�����������b=��Ȼ��b��ֵ���벻��ʽ2��b��1��ͨ����ò���ʽ�������a��ȡֵ��Χ4��a��2��
�ʴ�Ϊ��4��a��2. ����˵���У�������ǣ�������
A. ����ʽx��2������������һ��
B. -2�Dz���ʽ2x-1��0��һ����
C. ����ʽ-3x��9�Ľ⼯��x��-3
D. ����ʽx��10����������������
 C
������������������ⲻ��ʽ���B��C����ѡ��IJ���ʽ�Ľ⼯�������ж�C�������ɲ���ʽ��Ķ��壬�ж�B��ȷ��Ȼ���ɲ���ʽ�������֪ʶ�������ж�A��D��ȷ�������ô𰸣�
��������
A������ʽx��2����������ֻ��1����A��ȷ��
B��2x��1��0�Ľ⼯Ϊx�������ԩ�2�Dz���ʽ2x��1��0��һ���⣬��B��ȷ��
C������ʽ��3x��9�Ľ⼯��x����3����C����
D������...
C
������������������ⲻ��ʽ���B��C����ѡ��IJ���ʽ�Ľ⼯�������ж�C�������ɲ���ʽ��Ķ��壬�ж�B��ȷ��Ȼ���ɲ���ʽ�������֪ʶ�������ж�A��D��ȷ�������ô𰸣�
��������
A������ʽx��2����������ֻ��1����A��ȷ��
B��2x��1��0�Ľ⼯Ϊx�������ԩ�2�Dz���ʽ2x��1��0��һ���⣬��B��ȷ��
C������ʽ��3x��9�Ľ⼯��x����3����C����
D������... ���ı���ABCD�У���A����C��90�㣬��B���D�Ķ�������3��2�����B����D�Ķ�����
 ��B��108�㣬��D��72�㣮
������������������֪��A=��C=90��,���õ���B+��D=180��,�ٸ�����֪�ġ�B:��D=3:2,�������.
���������
�ߡ� A ���� C ��90�㣫90�㣽180�㣬��� B ���� D ��360�㣭(�� A ���� C )��360�㣭1 80�㣽180�㣮��� B ��( 3 x )�㣬��� D ��(2 x )�㣬��(3 x )�㣫(2 x )...
��B��108�㣬��D��72�㣮
������������������֪��A=��C=90��,���õ���B+��D=180��,�ٸ�����֪�ġ�B:��D=3:2,�������.
���������
�ߡ� A ���� C ��90�㣫90�㣽180�㣬��� B ���� D ��360�㣭(�� A ���� C )��360�㣭1 80�㣽180�㣮��� B ��( 3 x )�㣬��� D ��(2 x )�㣬��(3 x )�㣫(2 x )... ��ͼ����D��C��A��ͬһ��ֱ���ϣ��ڡ�ABC�У���A�á�ABC�á�ACB��3��5��10������EDC�ա�ABC�����BCE�Ķ���Ϊ��.
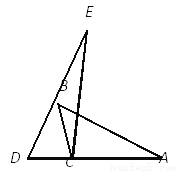
 20��
�����������������ε����ǵıȡ�A����ABC����ACB=3��5��10�����A=3x�㣬���ABC=5x�㣬��ACB=10x�㣬���������ε��ڽǺ�Ϊ180���3x+5x+10x=180�����x=10��������ǵĶ�����A=30�㣬��ABC=50�㣬��ACB=100�㣬�ɵá�BCN=180��-100��=80�㣬���ɡ�MNC�ա�ABC�õ���ACB=��MCN=100�㣬��˿���á�BCM=��NC...
20��
�����������������ε����ǵıȡ�A����ABC����ACB=3��5��10�����A=3x�㣬���ABC=5x�㣬��ACB=10x�㣬���������ε��ڽǺ�Ϊ180���3x+5x+10x=180�����x=10��������ǵĶ�����A=30�㣬��ABC=50�㣬��ACB=100�㣬�ɵá�BCN=180��-100��=80�㣬���ɡ�MNC�ա�ABC�õ���ACB=��MCN=100�㣬��˿���á�BCM=��NC... ����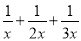 ���ڣ� ��
���ڣ� ��
A. 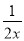 B.
B. 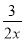 C.
C. 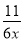 D.
D. 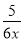
 C
�����������������
��
����
��ѡC��
C
�����������������
��
����
��ѡC�� ��ͼ����ACE����ƽ���ı���ABCD�ĶԽ���ACΪ�ߵĵȱ������Σ���C���E����x��Գƣ�CE��x���ڵ�H����E���������(7��һ3 )����D���������__________��
)����D���������__________��

 (5��0)
�������������������ͼ����EC��x�ύ�ڵ�Q,�ɵ�C���E����x��Գƿɵó���7��3����CE=6�����ACE���ԡ�ABCD�ĶԽ���ACΪ�ߵĵȱ������Σ�����AC=CE=6�����ݹ��ɶ����������AQ�ij�Ϊ9������OQ=7������OA=DQ=2�������OD=5�����ɵ�D��������ǣ�5,0����
(5��0)
�������������������ͼ����EC��x�ύ�ڵ�Q,�ɵ�C���E����x��Գƿɵó���7��3����CE=6�����ACE���ԡ�ABCD�ĶԽ���ACΪ�ߵĵȱ������Σ�����AC=CE=6�����ݹ��ɶ����������AQ�ij�Ϊ9������OQ=7������OA=DQ=2�������OD=5�����ɵ�D��������ǣ�5,0���� 
