题目内容
11.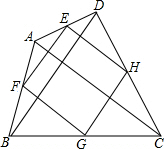 如图,四边形ABCD,将其四边的中点依次连结起来,得到一个新的四边形,这个新的四边形形状一定是平行四边形,连接它的对角线,则:
如图,四边形ABCD,将其四边的中点依次连结起来,得到一个新的四边形,这个新的四边形形状一定是平行四边形,连接它的对角线,则:(1)添加条件AC=BD,四边形EFGH是菱形.
(2)添加条件AC⊥BD,四边形ABCD是矩形,请证明(2)的正确性.
分析 根据三角形中位线定理得到EF∥HG,EF=HG,根据平行四边形的判定定理得到答案;
(1)根据邻边相等的平行四边形是菱形解得即可;
(2)根据一个角是直角的平行四边形是矩形解答即可.
解答 解:∵E、F分别是AD、AB的中线,
∴EF∥BD,EF=$\frac{1}{2}$BD,
同理HG∥BD,HG=$\frac{1}{2}$BD,
∴EF∥HG,EF=HG,
∴四边形EFGH是平行四边形;
(1)AC=BD,
∵EF=$\frac{1}{2}$BD,EH=$\frac{1}{2}$AC,
∴EF=EH,
∴平行四边形EFGH是菱形;
(2)AC⊥BD,
∵EF∥BD,
∴EF⊥AC,
∵EH∥AC,
∴EF⊥EH,即∠FEH=90°,
∴平行四边形EFGH是矩形.
故答案为:平行四边形;(1)AC=BD;(2)AC⊥BD.
点评 本题考查的是三角形中位线定理的应用、平行四边形、矩形、菱形的判定,掌握三角形的中位线平行于第三边且等于第三边的一半、灵活运用平行四边形、矩形、菱形的判定定理是解题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
2.如果两个相似三角形对应高的比为3:5,面积之比为2:x,那么x的算术平方根为( )
| A. | $\frac{5\sqrt{2}}{3}$ | B. | $±\frac{5\sqrt{2}}{3}$ | C. | $\frac{50}{9}$ | D. | $±\frac{50}{9}$ |
19.对角线互相平分的四边形一定是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
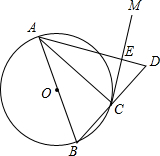 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.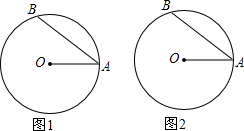 如图,⊙O的半径OA=5cm,AB是弦,∠OAB=30°,现有一动点C从A出发,沿弦AB运动到B,再从B沿劣弧BA回到点A.
如图,⊙O的半径OA=5cm,AB是弦,∠OAB=30°,现有一动点C从A出发,沿弦AB运动到B,再从B沿劣弧BA回到点A.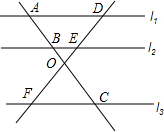 已知:l1∥l2∥l3,
已知:l1∥l2∥l3,