题目内容
18. 在如图所示的正方形网格中,每个小正方形的边长皆为1.请在网格上画出长度分别为$\sqrt{2}$,$\sqrt{5}$,$\sqrt{17}$的线段.
在如图所示的正方形网格中,每个小正方形的边长皆为1.请在网格上画出长度分别为$\sqrt{2}$,$\sqrt{5}$,$\sqrt{17}$的线段.
分析 由勾股定理得出:$\sqrt{2}$是直角边长为1,1的直角三角形的斜边;$\sqrt{5}$是直角边长为1,2的直角三角形的斜边;$\sqrt{17}$是直角边长为1,4的直角三角形的斜边.
解答  解:如图所示,图中的AB,CD,EF即为所求,
解:如图所示,图中的AB,CD,EF即为所求,
AB=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,CD=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,EF=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$.
点评 本题考查了勾股定理;解决本题的关键是找到无理数是直角边长为哪两个有理数的直角三角形的斜边长.

练习册系列答案
相关题目
8.将抛物线y=2x2先向右平移4个单位,再向上平移5个单位,得到的新抛物线的解析式为( )
| A. | y=2(x+4)2+5 | B. | y=2(x-4)2+5 | C. | y=2(x+4)2-5 | D. | y=2(x-4)2-5 |
6. 如图,数轴上点A,B表示的数分别为-40,50.现有一动点P以2个单位每秒的速度从点A向B运动,另一动点Q以3个单位每秒的速度从点B向A运动.当AQ=3PQ时,运动的时间为( )
如图,数轴上点A,B表示的数分别为-40,50.现有一动点P以2个单位每秒的速度从点A向B运动,另一动点Q以3个单位每秒的速度从点B向A运动.当AQ=3PQ时,运动的时间为( )
 如图,数轴上点A,B表示的数分别为-40,50.现有一动点P以2个单位每秒的速度从点A向B运动,另一动点Q以3个单位每秒的速度从点B向A运动.当AQ=3PQ时,运动的时间为( )
如图,数轴上点A,B表示的数分别为-40,50.现有一动点P以2个单位每秒的速度从点A向B运动,另一动点Q以3个单位每秒的速度从点B向A运动.当AQ=3PQ时,运动的时间为( )| A. | 15秒 | B. | 20秒 | C. | 15秒或25秒 | D. | 15秒或20秒 |
3.已知∠α是锐角,∠β是钝角,且∠α+∠β=180°,那么下列结论正确的是( )
| A. | ∠α的补角和∠β的补角相等 | B. | ∠α的余角和∠β的补角相等 | ||
| C. | ∠α的余角和∠β的补角互余 | D. | ∠α的余角和∠β的补角互补 |
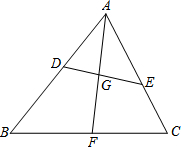 如图,在△ABC中,D,E分别是AB,AC上的点,∠AED=∠ABC,∠BAC的平分线AF交DE于点G,交BC于点F.
如图,在△ABC中,D,E分别是AB,AC上的点,∠AED=∠ABC,∠BAC的平分线AF交DE于点G,交BC于点F.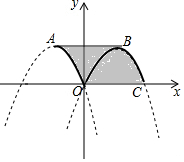 已知函数y=$\left\{\begin{array}{l}{-(x+1)^{2}+1(-1≤x<0)}\\{-(x-1)^{2}+1(0≤x≤2)}\end{array}\right.$,其图象如图中的实线部分,图象上两个最高点分别是A,B,连接AB,则图中曲四边形ABCO(阴影部分)的面积是2.
已知函数y=$\left\{\begin{array}{l}{-(x+1)^{2}+1(-1≤x<0)}\\{-(x-1)^{2}+1(0≤x≤2)}\end{array}\right.$,其图象如图中的实线部分,图象上两个最高点分别是A,B,连接AB,则图中曲四边形ABCO(阴影部分)的面积是2.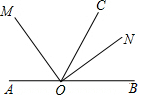 如图,点O是直线AB上一点,OM平分∠AOC,ON平分∠BOC.
如图,点O是直线AB上一点,OM平分∠AOC,ON平分∠BOC.