题目内容
12．已知某二次函数的图象是由二次函数y=2x2的图象平移后得到的，并且该二次函数的对称轴是x=1，同时该二次函数的图象经过点（3，2），求这个二次函数的解析式．分析 根据平移的性质可以设该二次函数为y=2（x-1）2+b，把点（3，2）代入，利用待定系数法求该函数解析式即可．
解答 解：依题意可以设该二次函数为y=2（x-1）2+b，
把点（3，2）代入，得
2=2（3-1）2+b，
解得b=-6．
故该二次函数解析式为：y=2（x-1）2-6．
点评 本题考查函数图象的平移、用待定系数法求函数解析式，以及一般表示法转换为顶点式．需找到相应的抛物线上的点．
练习册系列答案
相关题目
3．
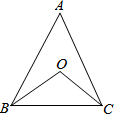如图，△ABC中，∠A=α°，BO、CO分别是∠ABC、∠ACB的平分线，则∠BOC的度数是（ ）
如图，△ABC中，∠A=α°，BO、CO分别是∠ABC、∠ACB的平分线，则∠BOC的度数是（ ）| A． | 2α° | B． | （α+60）° | C． | （α+90）° | D． | （$\frac{1}{2}$α+90）° |
4．抛物线y=-3x2+2x-l的图象与坐标轴的交点个数是（ ）
| A． | 无交点 | B． | 1个 | C． | 2个 | D． | 3个 |
2．在下列说法中，正确的是（ ）
| A． | 如果两个三角形全等，则它们一定能关于某直线成轴对称 | |
| B． | 如果两个三角形关于某直线成轴对称，那么它们是全等三角形 | |
| C． | 等腰三角形的对称轴是底边上的高 | |
| D． | 若两个图形关于某直线对称，则它们的对应点一定位于对称轴的两侧 |