题目内容
3.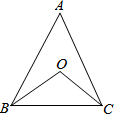 如图,△ABC中,∠A=α°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
如图,△ABC中,∠A=α°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )| A. | 2α° | B. | (α+60)° | C. | (α+90)° | D. | ($\frac{1}{2}$α+90)° |
分析 根据三角形的内角和定理和角平分线的定义求出∠OBC+∠OCB的度数,再根据三角形的内角和等于180°,即可求出∠BOC的度数.
解答 解:∵∠A=α°,
∴∠ABC+∠ACB=180°-∠A=180°-α,
∵BO,CO分别是∠ABC,∠ACB的平分线,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×(180°-α)=90°-$\frac{1}{2}$α,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-$\frac{1}{2}$α)=$\frac{1}{2}$α+90°.
故选:D
点评 本题主要利用三角形的内角和定理和角平分线的定义,熟练掌握定理和概念是解题的关键.

练习册系列答案
相关题目
13.若x为有理数,x-|x|表示的数是( )
| A. | 正数 | B. | 非正数 | C. | 负数 | D. | 非负数 |
11.多项式6πa3b2c2-x3y3z+m2n-110的次数是( )
| A. | 10次 | B. | 8次 | C. | 7次 | D. | 9次 |
18.由二次函数y=3(x-2)2+1可知( )
| A. | 图象的开口向下 | B. | 图象的对称轴是直线x=-2 | ||
| C. | 函数最小值为1 | D. | 当x<2时,y随x的增大而增大 |
 中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.
中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.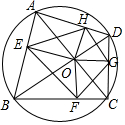 如图,O为圆内接四边形ABCD对角线的交点,OE⊥AB.OF⊥BC,OG⊥CD,OA⊥DA,求证:EH+FG=EF+HG.
如图,O为圆内接四边形ABCD对角线的交点,OE⊥AB.OF⊥BC,OG⊥CD,OA⊥DA,求证:EH+FG=EF+HG.