题目内容

5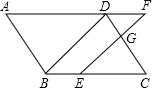．如图，在?ABCD中，点E在边BC上，点F在边AD的延长线上，且DF=BE=4，连接EF交CD于G．若$\frac{DG}{GC}$=$\frac{2}{3}$，求AD的长．

分析 根据相似三角形的判定与性质，可得答案．

解答 证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∵DF∥EC，
∴△DFG∽CEG，
∴$\frac{DF}{CE}$=$\frac{DG}{GC}$=$\frac{2}{3}$，
∴CE=6，
∴AD=BC=BE+CE=10．

点评 本题考查了平行四边形的性质，相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．

练习册系列答案
相关题目
15．关于x的一元二次方程x2+（2k+1）x+k2+1=0有两个不等实根x1，x2．
（1）求实数k的取值范围；
（2）若方程两实根x1，x2满足x1+x2=-x1x2，求k的值．
16．解下列方程：
（1）4-x=7x+6
（2）$\frac{2x-1}{3}$-$\frac{x+1}{4}$=4．
13．小明爸爸骑着摩托车带着小明在公路上匀速行驶，小明每隔一小时看到的里程碑上的数字情况如下：12：00时，这是两位数，它的两个数字之和为7，13：00时，十位与个位数字与12：00时看到的正好颠倒了；14：00时，比12：00时看到的两位数中间多了个0，请你求出小明在12：00时看到的里程碑上的数字．
20．如图，射线OA⊥OC，射线OB⊥OD，则图中互为补角的对数共有（　　）
A．1对B．2对C．3对D．4对
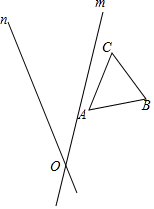10．如图，直线m，n的夹角为35°，相交于点O，
（1）作出△ABC关于直线m的对称△DEF；
（2）作出△DEF关于直线n的对称△PQR；
（3）△PQR还可以由△ABC经过一次怎样的变换得到．
17．（1）如图（1），△ABC中，分别以AC、BC为边作等边△ACE，等边△BCD，连接AD、BE交于点P，猜想线段AD和BE之间的数量关系是AD=BE，∠BPD的度数为60°．（不必证明）
（2）如图（2），△ABC中，∠ABC=45°，AB=3，BC=5，分别以AC、BC为边作等腰Rt△ACE，等腰Rt△BCD，使AC=CE，BC=CD，∠ACE=∠BCD=90°，连AD、BE，求BE的长．
（3）如图（3），△ABC中，AC=2，分别以AC、BC为边作Rt△ACE，Rt△BCD，使∠ACE=∠BCD=90°，∠AEC=∠CBD=30°，连接AD、BE、DE，若∠CAD=30°，DE=5，求BE的长．
14．一个正方体的每个面都有一个汉字，其平面展开图如图所示，那么，在该正方体中与“设”字相对的字是（　　）
A．美B．丽C．盐D．城
15．如图，直线AB、CD相交于点O，OE平分∠BOD，∠AOC=74°，∠DOF=90°．
求：
（1）∠BOC的度数；
（2）∠BOE的度数；
（3）∠EOF的度数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网