题目内容
 如图,A是半径为1的⊙O的外一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥AO,连结AC,则图中的阴影部分的面积等于
如图,A是半径为1的⊙O的外一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥AO,连结AC,则图中的阴影部分的面积等于考点:切线的性质,扇形面积的计算
专题:
分析:△OBC与△BCA是同底等高,则它们的面积相等,因此阴影部分的面积实际是扇形OCB的面积;扇形OCB中,已知了半径的长,关键是圆心角∠COB的度数.在Rt△ABO中,根据OB、OA的长,即可求得∠BOA的度数;由于OA∥BC,也就求得了∠OBC的度数,进而可在△COB中求出∠COB的度数,由此可根据扇形的面积公式求出阴影部分的面积.
解答: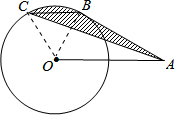 解:OB是半径,AB是切线,
解:OB是半径,AB是切线,
∵OB⊥AB,
∴∠ABO=90°,
∴sinA=
=
,
∴∠A=30°,
∵OC=OB,BC∥OA,
∴∠OBC=∠BOA=60°,
∴△OBC是等边三角形,
因此S阴影=S扇形CBO=
=
.
故答案为
.
 解:OB是半径,AB是切线,
解:OB是半径,AB是切线,∵OB⊥AB,
∴∠ABO=90°,
∴sinA=
| OB |
| OA |
| 1 |
| 2 |
∴∠A=30°,
∵OC=OB,BC∥OA,
∴∠OBC=∠BOA=60°,
∴△OBC是等边三角形,
因此S阴影=S扇形CBO=
| 60π×1 |
| 360 |
| π |
| 6 |
故答案为
| π |
| 6 |
点评:本题利用了平行线的性质,同底等高的三角形面积相等,切线的概念,正弦的概念,扇形的面积公式求解.

练习册系列答案
相关题目
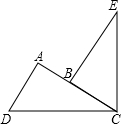 如图,已知∠DCE=90°,∠DAC=90°,BE⊥AC于B,且DC=EC,若BE=7,AB=3,则AD的长为( )
如图,已知∠DCE=90°,∠DAC=90°,BE⊥AC于B,且DC=EC,若BE=7,AB=3,则AD的长为( )| A、3 | B、5 | C、4 | D、不确定 |
 如图是一块地,已知AD=8cm,CD=6cm,∠D=90°,AB=26cm,BC=24cm,求这块地的面积.
如图是一块地,已知AD=8cm,CD=6cm,∠D=90°,AB=26cm,BC=24cm,求这块地的面积. 如图,PA、PB是圆O的切线,切点分别为A、B,探索∠AOB与∠PAB之间的数量关系,并说明理由.
如图,PA、PB是圆O的切线,切点分别为A、B,探索∠AOB与∠PAB之间的数量关系,并说明理由.