题目内容
3.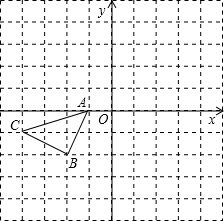 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1;
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2;则A2(1,0),B2(2,2),C2(4,1).
分析 (1)根据网格结构找出点B、C绕点A顺时针旋转90°的对应点B1、C1的位置,然后与点A顺次连接即可;
(2)根据网格结构找出点A、B、C关于点O的对称点A2、B2、C2的位置,然后顺次连接即可
解答  解:(1)△AB1C1如图所示;
解:(1)△AB1C1如图所示;
(2)△A2B2C2如图所示.
A2( 1,0 ),B2(2,2),C2 (4,1).
故答案为:( 1,0 ),(2,2),(4,1).
点评 本题考查的是作图-旋转变换,熟练掌握网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
11.已知甲乙两组各10个数据的平均数都是8,甲组数据的方差S甲2=0.12,乙组数据的方差 S乙2=0.5,则( )
| A. | 甲组数据的波动大 | B. | 乙组数据的波动大 | ||
| C. | 甲乙两组数据的波动一样大 | D. | 甲乙两组数据的波动大小不能比较 |
18.为了解某校八年级学生每天干家务活的平均时间,小颖同学在该校八年级每班随机调查5名学生,统计这些学生2016年2月每天干家务活的平均时间(单位:min).
(1)统计表中的a=25;b=12.5%;c=40;
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)该校八年级共有240名学生,求每天干家务活的平均时间在11-20min的学生人数.
| 干家务活平均时间 | 频数 | 百分比 |
| A(0-10min) | 10 | 25% |
| B(11-20min) | a | 62.5% |
| C(21-30min) | 5 | b |
| 合 计 | c | 100% |
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)该校八年级共有240名学生,求每天干家务活的平均时间在11-20min的学生人数.
15.如果分式$\frac{{{x^2}-4}}{x+2}$的值为零,则x的值为( )
| A. | 2 | B. | -2 | C. | 0 | D. | ±2 |