题目内容
8.计算:$\sqrt{0.25}+{(2\sqrt{2}-3)^{-1}}+|{2\sqrt{2}-\frac{1}{2}}|+{(π-\sqrt{2})^0}$.分析 首先利用负整数指数幂的性质以及零指数幂的性质、绝对值的性质、二次根式的性质分别化简进而求出答案.
解答 解:原式=$\frac{1}{2}$+$\frac{1}{{2\sqrt{2}-3}}$+2$\sqrt{2}$-$\frac{1}{2}$+1
=$\frac{1}{2}$-2$\sqrt{2}$-3+2$\sqrt{2}$-$\frac{1}{2}$+1
=-2.
点评 此题主要考查了二次根式的加减运算以及负整数指数幂的性质以及零指数幂的性质等知识,正确化简各数是解题关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
18.一组数据1、2、8、17、45的中位数为( )
| A. | 1 | B. | 2 | C. | 8 | D. | 17 |
13.某电脑公司现有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌的电脑中各选购一种型号的电脑.
(1)写出所有选购方案(利用树状图或列表方法表示);
(2)如果(1)中各种选购方案被选中的可能性相同,那么A型电脑被选中的概率是多少?
(3)现知希望中学购买甲、乙两种品牌的电脑共36台(价格如表所示),恰好用了10万元人民币,其中甲品牌电脑为A型号电脑,求购买的A型号电脑有多少台?
| XX电脑公司电脑单价 |
| 单位(元) |
| A型:6000 |
| B型:4000 |
| C型:2500 |
| D型:5000 |
| E型:2000 |
(2)如果(1)中各种选购方案被选中的可能性相同,那么A型电脑被选中的概率是多少?
(3)现知希望中学购买甲、乙两种品牌的电脑共36台(价格如表所示),恰好用了10万元人民币,其中甲品牌电脑为A型号电脑,求购买的A型号电脑有多少台?
17.从3,1,-2这三个数中任取两个不同的数作为M点的坐标,则M点刚好落在第一象限的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |

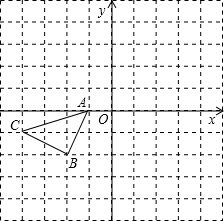 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: