题目内容
7.计算(1)$-8×(-\frac{1}{6}+\frac{3}{4}-\frac{1}{12})÷\frac{1}{6}$
(2)$-{4^3}÷(-32)-[{{{({-\frac{2}{3}})}^3}×(-{3^2})+(-\frac{11}{3})}]$
(3)$11.35×{(-\frac{2}{3})^2}+1.05×(-\frac{2^2}{9})-7.7×(-\frac{4}{3^2})$.
分析 (1)根据乘法分配律可以解答本题;
(2)根据幂的乘方、有理数的乘除法和加减法可以解答本题;
(3)根据幂的乘方、有理数的乘法和加减法可以解答本题.
解答 解:(1)$-8×(-\frac{1}{6}+\frac{3}{4}-\frac{1}{12})÷\frac{1}{6}$
=$-8×(-\frac{1}{6}+\frac{3}{4}-\frac{1}{12})×6$
=$-48×(-\frac{1}{6}+\frac{3}{4}-\frac{1}{12})$
=8-36+4
=-24;
(2)(2)$-{4^3}÷(-32)-[{{{({-\frac{2}{3}})}^3}×(-{3^2})+(-\frac{11}{3})}]$
=$-64÷(-32)-[{-\frac{8}{27}×(-9)-\frac{11}{3}}]$
=$2-(\frac{8}{3}-\frac{11}{3})$
=2-(-1)
=3;
(3)$11.35×{(-\frac{2}{3})^2}+1.05×(-\frac{2^2}{9})-7.7×(-\frac{4}{3^2})$
=$11.35×\frac{4}{9}+1.05×(-\frac{4}{9})-7.7×(-\frac{4}{9})$
=$11.35×\frac{4}{9}-1.05×\frac{4}{9}+7.7×\frac{4}{9}$
=$(11.35-1.05+7.7)×\frac{4}{9}$
=$\frac{80}{9}$.
点评 本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
17.下列多项式的乘法中,可用平方差公式计算的是( )
| A. | (a-b)(-a+b) | B. | (x2-y)(y2-x) | C. | ($\frac{1}{2}$a+b)(b-$\frac{1}{2}$a) | D. | (a+b)(-a-b) |
18.若a>b,则下列各不等式中不成立的是( )
| A. | a-1<b-1 | B. | $\frac{1}{8}$a>$\frac{1}{8}$b | C. | -8a<-8b | D. | -1-a<-1-b |
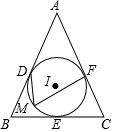 如图,⊙I与△ABC的三边分别切于点D、E、F,∠B=70°,∠C=60°,M是$\widehat{DEF}$上的动点(与D、E不重合),∠DMF的度数为65°.
如图,⊙I与△ABC的三边分别切于点D、E、F,∠B=70°,∠C=60°,M是$\widehat{DEF}$上的动点(与D、E不重合),∠DMF的度数为65°.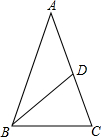 (1)等腰三角形一腰上的中线将这个等腰三角形的周长分成15cm和6cm两部分.求等腰三角形的底边长.
(1)等腰三角形一腰上的中线将这个等腰三角形的周长分成15cm和6cm两部分.求等腰三角形的底边长.