题目内容
9.化简:($\frac{a}{a+2}$+$\frac{1}{{a}^{2}-1}$)÷$\frac{a-1}{a+2}$=$\frac{{a}^{3}+2}{(a+1)(a-1)^{2}}$.分析 先计算括号,后计算乘除即可.
解答 解:原式=[$\frac{{a}^{3}-a}{(a+2)({a}^{2}-1)}$+$\frac{a+2}{(a+2)({a}^{2}-1)}$]•$\frac{a+2}{a-1}$
=$\frac{{a}^{3}+2}{({a}^{2}-1)(a-1)}$
=$\frac{{a}^{3}+2}{(a+1)(a-1)^{2}}$.
点评 本题考查分式的混合运算法则,正确运用法则是解题的关键.

练习册系列答案
相关题目
17.x>-y,则下列不等式中成立的有( )
| A. | x+y<0 | B. | x-y>0 | C. | a2x>-a2y | D. | 3x+3y>0 |
18.点A(-2,a)是抛物线y=x2上一点,则下列各点在抛物线y=x2上的是( )
| A. | (-2,-a) | B. | (2,a) | C. | (2,-a) | D. | (a,-2) |
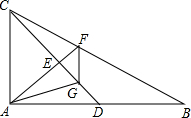 如图,在Rt△ABC中,E为CD的中点,FG∥AC.
如图,在Rt△ABC中,E为CD的中点,FG∥AC.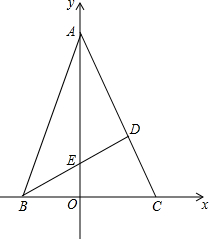 如图,在坐标系中,A(0,6),B(-2,0),C(3,0),∠BAC=45°,BD⊥AC,M(4,6),动点P从点M出发,沿x轴正方向,以每秒2个单位的长度运动t秒
如图,在坐标系中,A(0,6),B(-2,0),C(3,0),∠BAC=45°,BD⊥AC,M(4,6),动点P从点M出发,沿x轴正方向,以每秒2个单位的长度运动t秒