题目内容
18.点A(-2,a)是抛物线y=x2上一点,则下列各点在抛物线y=x2上的是( )| A. | (-2,-a) | B. | (2,a) | C. | (2,-a) | D. | (a,-2) |
分析 根据二次函数图象上点的坐标特征,把A(-2,a)代入抛物线解析式即可求出a的值,然后将四个选项中的坐标代入抛物线方程中,看两边是否相等,即可判断该点是否在抛物线上.
解答 解:A(-2,a)代入y=x2得a=4,
A.-4≠(-2)2,故(-2,-a)不在抛物线上.
B.4=22,故(2,a)在抛物线上.
C.-4≠22,故(2,-a)不在抛物线上.
D.-2≠42,故(a,-2)不在抛物线上.
故选B.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
8.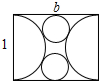 如图,用邻边分别为1,b(b>1)的矩形硬纸板裁出以1为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆,把半圆作为圆锥的侧面,小圆恰好作为底面,从而做成两个圆锥(拼接处材料忽略不计),则b的值为( )
如图,用邻边分别为1,b(b>1)的矩形硬纸板裁出以1为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆,把半圆作为圆锥的侧面,小圆恰好作为底面,从而做成两个圆锥(拼接处材料忽略不计),则b的值为( )
 如图,用邻边分别为1,b(b>1)的矩形硬纸板裁出以1为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆,把半圆作为圆锥的侧面,小圆恰好作为底面,从而做成两个圆锥(拼接处材料忽略不计),则b的值为( )
如图,用邻边分别为1,b(b>1)的矩形硬纸板裁出以1为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆,把半圆作为圆锥的侧面,小圆恰好作为底面,从而做成两个圆锥(拼接处材料忽略不计),则b的值为( )| A. | b=$\sqrt{3}$ | B. | b=$\frac{\sqrt{5}+1}{2}$ | C. | b=$\frac{\sqrt{5}}{2}$ | D. | b=$\sqrt{2}$ |
7.将2016加上它本身的$\frac{1}{2}$的相反数,再将这个结果加上其$\frac{1}{3}$的相反数,再将上述结果加上其$\frac{1}{4}$的相反数,…,如此继续.操作2015次后所得的结果是( )
| A. | 0 | B. | 1 | C. | $\frac{2016}{2015}$ | D. | 2015 |
 如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD的度数是32°.
如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD的度数是32°.