题目内容
7.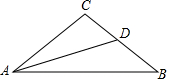 已知:如图,在△ABC中,AC=BC,∠C=100°,AD平分∠CAB.
已知:如图,在△ABC中,AC=BC,∠C=100°,AD平分∠CAB.求证:AD+CD=AB.
分析 如图,在AB上截取BE=AC,延长AD到F使AF=AB,连接DE、BF,只要证明△ABC≌△ADE,△DBE≌△DBF,即可解决问题.
解答 证明:如图,在AB上截取BE=AC,延长AD到F使AF=AB,连接DE、BF.
又∵∠1=∠2,AD是公共边BE,
在△ADC和△ADE中,
$\left\{\begin{array}{l}{AC=AE}\\{∠1=∠2}\\{AD=AD}\end{array}\right.$,
∴△ABC≌△ADE,
∴∠AED=∠C=100°,则得∠DEB=80°
∵CA=CB,AD平分∠BAC,
∴∠1=∠2=20°,∠3=40°
∵AF=AB,∠2=20°,
∴∠F=∠ABF=1/2(180°-∠2)=80°则∠F=∠DEB
∴∠4=80°-∠3=40°,
∴∠3=∠4,∠F=∠DEC,
在△BDF和△BDE中,
$\left\{\begin{array}{l}{∠3=∠4}\\{∠DEB=∠F}\\{BD=BD}\end{array}\right.$,
∴△DBE≌△DBF(AAS)
∴DF=DE=CD
∴AB=AF=AD+DF=AD+DC.
点评 本题考查全等三角形的判定和性质、解题的关键是学会利用截长补短法添加辅助线构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
15.如图,在数轴上表示互为相反数的两数的点是( )


| A. | 点A和点C | B. | 点B和点A | C. | 点C和点B | D. | 点D和点B |
2.在数轴上a所对应的点与b所对应的点相差6个单位长度,若-a=2,则b等于( )
| A. | 4 | B. | -4 | C. | -8 | D. | 4或-8 |
16.已知一直角三角形的斜边比一直角边大2,另一条直角边长为6,那么斜边长为( )
| A. | 4 | B. | 8 | C. | 10 | D. | 12 |
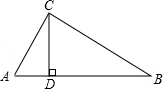 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=30°,CD=6,求AB的长.
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=30°,CD=6,求AB的长.