题目内容
5.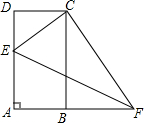 如图,在矩形ABCD中,AD=8,AB=4,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠AFE的余弦值为$\frac{2\sqrt{5}}{5}$.
如图,在矩形ABCD中,AD=8,AB=4,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠AFE的余弦值为$\frac{2\sqrt{5}}{5}$.
分析 根据翻折变换的性质结合勾股定理首先求出AE的长,进而得出AF,EF的长,再利用锐角三角函数关系得出答案.
解答  解:设AE=x,则EC=x,DE=8-x,
解:设AE=x,则EC=x,DE=8-x,
故DE2+DC2=EC2,
则(8-x)2+42=x2,
解得:x=5,
则EC=AE=5,DE=3,
设BF=y,则AF=FC=4+y,
故BC2+BF2=FC2,
则82+y2=(4+y)2,
解得:y=6,
故AF=10,
则EF=$\sqrt{1{0}^{2}+{5}^{2}}$=5$\sqrt{5}$,
故cos∠AFE=$\frac{AF}{EF}$=$\frac{10}{5\sqrt{5}}$=$\frac{2}{5}$$\sqrt{5}$.
故答案为:$\frac{2}{5}\sqrt{5}$.
点评 此题主要考查了矩形的性质以及勾股定理等知识,根据题意得出BF,AE的长是解题关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
15.给出下列函数:①y=2x;②y=-2x+1;③y=$\frac{2}{x}$(x>0);④y=x2(x<1),其中y随x的增大而减小的函数是( )
| A. | ①②③④ | B. | ②③④ | C. | ②④ | D. | ②③ |

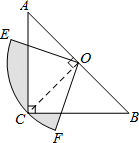 如图,在△ABC中∠C=90°,AC=BC=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为$\frac{1}{2}$π-1.
如图,在△ABC中∠C=90°,AC=BC=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为$\frac{1}{2}$π-1.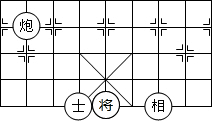 中国象棋在中国有着三千多年的历史,它难易适中,趣味性强,变化丰富细腻,棋盘棋子文字都体现了中国文化.如图,如果
中国象棋在中国有着三千多年的历史,它难易适中,趣味性强,变化丰富细腻,棋盘棋子文字都体现了中国文化.如图,如果 所在位置的坐标为(-1,-1),
所在位置的坐标为(-1,-1), 所在位置的坐标为(2,-1),那么,
所在位置的坐标为(2,-1),那么, 所在位置的坐标为(-3,2).
所在位置的坐标为(-3,2).