题目内容
6．小红准备了五张形状、大小完全相同的不透明卡片，正面分别写-3、-1、0、1、3，将这五张卡片的正面朝下在桌面上，从中任意抽取一张，将卡片上的数字记为m，再从剩下的卡片中任取一张卡片并把数字记为n，恰好使得关于x、y的二元一次方程组$\left\{\begin{array}{l}2x-y=n\\ mx+y=1\end{array}\right.$有整数解的概率为$\frac{1}{2}$．分析 列表或树状图将所有等可能的结果列举出来，然后利用概率公式求解即可．
解答 解：列表如下：
| -3 | -1 | 0 | 1 | 3 | |
| -3 | --- | （-1，-3） | （0，-3） | （1，-3） | （3，-3） |
| -1 | （-3，-1） | --- | （0，-1） | （1，-1） | （3，-1） |
| 0 | （-3，0） | （-1，0） | --- | （1，0） | （3，0） |
| 1 | （-3，1） | （-1，1） | （0，1） | --- | （3，1） |
| 3 | （-3，3） | （-1，3） | （0，3） | （1，3） | --- |
∴使得关于x、y的二元一次方程组$\left\{\begin{array}{l}2x-y=n\\ mx+y=1\end{array}\right.$有整数解的概率为$\frac{1}{2}$，
故答案为：$\frac{1}{2}$．
点评 本题考查了列表法与树状图的知识，解题的关键是能够将所有等可能的结果列举出来．
练习册系列答案
相关题目
14．小芳掷一枚质地均匀的硬币10次，有7次正面向上，当她掷第11次时，正面向上的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{7}{10}$ | C． | $\frac{7}{11}$ | D． | 不能确定 |
11．
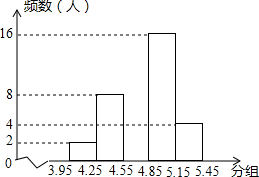青少年视力水平下降已引起全社会的广泛关注，为了了解某市5000名初中毕业生的视力情况．我们从中抽取了一部分学生的视力作为样本进行数据处理，得到如下的频数分布表和频数分布直方图：
（1）根据上述数据，补全频数分布直方图和频数分布表；
（2）若视力在4.85以上属于正常，不需矫正，试估计该市5000名初中毕业生中约有多少名学生的视力需要矫正．
青少年视力水平下降已引起全社会的广泛关注，为了了解某市5000名初中毕业生的视力情况．我们从中抽取了一部分学生的视力作为样本进行数据处理，得到如下的频数分布表和频数分布直方图：| 分组 | 频数 | 频率 |
| 3.95～4.25 | 2 | 0.04 |
| 4.25～4.55 | 8 | 0.16 |
| 4.55～4.85 | 20 | 0.40 |
| 4.85～5.15 | 16 | 0.32 |
| 5.15～5.45 | 4 | 0.08 |
| 合计 | 1 |
（2）若视力在4.85以上属于正常，不需矫正，试估计该市5000名初中毕业生中约有多少名学生的视力需要矫正．
阅读理解：对于任意正实数a，b，$Q（\sqrt{a}-\sqrt{b}）^{2}≥0$，
15．下列运算中正确的是（ ）
| A． | a5÷b5=1 | B． | a6•a4=a24 | C． | a4+b4=（a+b）4 | D． | （a2）3=a6 |