题目内容
16.(1)计算:$\sqrt{8}$+|$\sqrt{2}$-1|-π0+4sin30°;(2)解不等式组:$\left\{\begin{array}{l}{x-3<1}\\{4x-4≥x+2}\end{array}\right.$.
分析 (1)根据平方根、绝对值、0指数幂、特殊角的三角函数值解答;
(2)分别求出不等式的解集,求出公共部分即可.
解答 解:(1)原式=2$\sqrt{2}$+$\sqrt{2}$-1-1+4×$\frac{1}{2}$
=3$\sqrt{2}$;
(2)由x-3<1得x<4,
由4x-4≥x+2得,x≥2,
所以原不等式组的解为2≤x<4.
点评 (1)本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟悉平方根、绝对值、0指数幂、特殊角的三角函数值的计算;
(2)本题考查了不等式的计算,熟悉不等式的解法是解题的关键.

练习册系列答案
相关题目
6.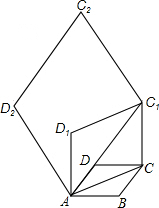 如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第六个菱形的边长为( )
如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第六个菱形的边长为( )
 如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第六个菱形的边长为( )
如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第六个菱形的边长为( )| A. | 9 | B. | 9$\sqrt{3}$ | C. | 27 | D. | 27$\sqrt{3}$ |
7.工人师傅在架设电线时,为了检验三条电线是否平行,工人师傅只检验其中两条是否与第三条平行即可,这种做法的依据是( )
| A. | 两点确定一条直线 | |
| B. | 两点之间,线段最短 | |
| C. | 经过直线外一点有且只有一条直线与已知直线平行 | |
| D. | 如果两条直线都和第三条直线平行,那么这两条直线也相互平行 |
11.若式子$\sqrt{x-7}$在实数范围内有意义,则x的取值范围是( )
| A. | x<7 | B. | x≤7 | C. | x>7 | D. | x≥7 |
5.若(xny•xym)5=x10y15,则3m(n+1)=( )
| A. | 12 | B. | 10 | C. | 8 | D. | 15 |
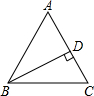 如图,在△ABC中,AB=AC,BD⊥AC于D,BD=4,CB=5,求AB的长.
如图,在△ABC中,AB=AC,BD⊥AC于D,BD=4,CB=5,求AB的长.