题目内容
6.若方程x2-3x+1=0有一个根为m,试求m2+$\frac{1}{{m}^{2}}$的值.分析 把x=m代入已知方程,得到m2-3m+1=0,两边同时除以m,得m+$\frac{1}{m}$=3,再两边平方运用完全平方公式即可求出m2+$\frac{1}{{m}^{2}}$的值.
解答 解:∵方程x2-3x+1=0有一个根为m,
∴m2-3m+1=0,
∴m≠0,
∴两边同时除以m,得m-3+$\frac{1}{m}$=0,即m+$\frac{1}{m}$=3,
两边平方得,(m+$\frac{1}{m}$)2=32,
∴m2+2+$\frac{1}{{m}^{2}}$=9,
∴m2+$\frac{1}{{m}^{2}}$=7.
点评 本题考查了一元二次方程的解的定义:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.求出m+$\frac{1}{m}$=3是解题的关键.

练习册系列答案
相关题目
17.已知一元二次方程:2x2-3x-4=0的两个根分别是x1、x2,则x12x2+x1x22的值为( )
| A. | -3 | B. | 3 | C. | -6 | D. | 6 |
 如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).你添加的条件是AE=AC.
如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).你添加的条件是AE=AC.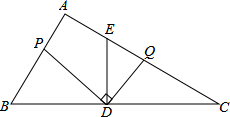 如图,在Rt△ABC中,∠A=90°,AB=12,AC=16,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.
如图,在Rt△ABC中,∠A=90°,AB=12,AC=16,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.