题目内容
8.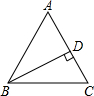 如图,在△ABC中,AB=AC,BD⊥AC于D,BD=4,CB=5,求AB的长.
如图,在△ABC中,AB=AC,BD⊥AC于D,BD=4,CB=5,求AB的长.
分析 在直角三角形BDC中,由BD与CB的长,利用勾股定理求出CD的长,在直角三角形ABC中,设AB=AC=x,由AC-CD表示出AD,在直角三角形ABD中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为AB的长.
解答 解:在Rt△BDC中,BD=4,CB=5,
根据勾股定理得:CD=$\sqrt{C{B}^{2}-B{D}^{2}}$=3,
在Rt△ABD中,设AB=AC=x,则有AD=AC-CD=x-3,
由勾股定理得:AB2=BD2+AD2,即x2=16+(x-3)2,
解得:x=$\frac{25}{6}$,
则AB的长为$\frac{25}{6}$.
点评 此题考查了勾股定理,利用了方程的思想,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
3. 如图为某几何体的示意图,则该几何体的俯视图为( )
如图为某几何体的示意图,则该几何体的俯视图为( )
 如图为某几何体的示意图,则该几何体的俯视图为( )
如图为某几何体的示意图,则该几何体的俯视图为( )| A. |  | B. |  | C. |  | D. |  |
17.已知一元二次方程:2x2-3x-4=0的两个根分别是x1、x2,则x12x2+x1x22的值为( )
| A. | -3 | B. | 3 | C. | -6 | D. | 6 |
 如图,抛物线y=ax2+bx+4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
如图,抛物线y=ax2+bx+4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G. 如图,以1个单位长度为边长画一个正方形,位置在整数点1到整数点2之间,以整数点1出为圆心,以正方形的对角线为半径,画弧,交数轴于A,B两点.
如图,以1个单位长度为边长画一个正方形,位置在整数点1到整数点2之间,以整数点1出为圆心,以正方形的对角线为半径,画弧,交数轴于A,B两点.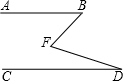 如图,已知AB∥CD,证明:∠BFD=∠B+∠D.(用两种方法证明)
如图,已知AB∥CD,证明:∠BFD=∠B+∠D.(用两种方法证明)