题目内容
6.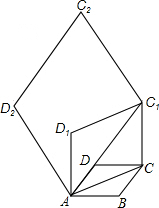 如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第六个菱形的边长为( )
如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第六个菱形的边长为( )| A. | 9 | B. | 9$\sqrt{3}$ | C. | 27 | D. | 27$\sqrt{3}$ |
分析 先求出第一个菱形和第二个菱形的边长,得出规律,根据规律即可得出结论.
解答 解:连接BD交AC于O,连接CD1交AC1于E,如图所示: ∵四边形ABCD是菱形,∠DAB=60°,
∵四边形ABCD是菱形,∠DAB=60°,
∴ACD⊥BD,∠BAO=$\frac{1}{2}$∠DAB=30°,
OA=$\frac{1}{2}$AC,
∴OA=AB•cos30°=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
∴AC=2OA=$\sqrt{3}$,
同理AE=AC•cos30°=$\sqrt{3}$•$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$,AC1=3=($\sqrt{3}$)2,…,
第n个菱形的边长为($\sqrt{3}$)n-1,
∴第六个菱形的边长为($\sqrt{3}$)5=9$\sqrt{3}$;
故选:B.
点评 本题考查了菱形的性质、含30°角的直角三角形以及锐角三角函数的运用;根据第一个和第二个菱形的边长得出规律是解决问题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
1. 如图所示,在△ABC中,AB=AC,AB的垂直平分线分别交AC、AB于D、E,若△ABC和△DBC的周长分别为40cm和25cm,则BC等于( )
如图所示,在△ABC中,AB=AC,AB的垂直平分线分别交AC、AB于D、E,若△ABC和△DBC的周长分别为40cm和25cm,则BC等于( )
 如图所示,在△ABC中,AB=AC,AB的垂直平分线分别交AC、AB于D、E,若△ABC和△DBC的周长分别为40cm和25cm,则BC等于( )
如图所示,在△ABC中,AB=AC,AB的垂直平分线分别交AC、AB于D、E,若△ABC和△DBC的周长分别为40cm和25cm,则BC等于( )| A. | 5cm | B. | 10cm | C. | 15cm | D. | 12cm |
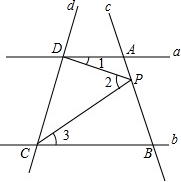 如图,已知直线c和a、b分别交于A、B两点,点P在直线c上运动.
如图,已知直线c和a、b分别交于A、B两点,点P在直线c上运动.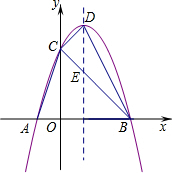 如图,抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴相交于点C,顶点为D.
如图,抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴相交于点C,顶点为D. 在所建立的平面直角坐标系中:
在所建立的平面直角坐标系中: 如图,抛物线y=ax2+bx+4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
如图,抛物线y=ax2+bx+4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.