题目内容
如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).
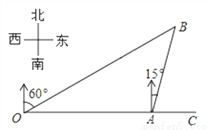
 【解析】试题分析:过点A作AD⊥OB于D.先解Rt△AOD,得出AD=OA=2km,再由△ABD是等腰直角三角形,得出BD=AD=2km,则AB=AD=km.
【解析】
如图,过点A作AD⊥OB于D.
在Rt△AOD中,
∵∠ADO=90°,∠AOD=30°,OA=4km,
∴AD=OA=2km.
在Rt△ABD中,∵∠ADB=90°,∠B=∠CAB?∠AOB=75...
【解析】试题分析:过点A作AD⊥OB于D.先解Rt△AOD,得出AD=OA=2km,再由△ABD是等腰直角三角形,得出BD=AD=2km,则AB=AD=km.
【解析】
如图,过点A作AD⊥OB于D.
在Rt△AOD中,
∵∠ADO=90°,∠AOD=30°,OA=4km,
∴AD=OA=2km.
在Rt△ABD中,∵∠ADB=90°,∠B=∠CAB?∠AOB=75...
练习册系列答案
相关题目
已知二次函数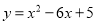 .
.
(1)解析式化为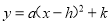 的形式;
的形式;
(2)求出该函数图象与x轴、y轴的交点坐标.
 (1)(2)(1,0),(5,0)|(0,5)
【解析】分析:(1)通过配方得到;(2)先把抛物线的解析式写成交点式得到=(x-1)(x-5),即可得到抛物线与x轴的交点坐标;把x=0代入原函数关系式可确定抛物线与y轴的交点坐标.
本题解析:(1);
(2)∵=(x-1)(x-5),
∴抛物线与x轴交点坐标为(1,0),(5,0);
令x=0,y=-5,
故抛物...
(1)(2)(1,0),(5,0)|(0,5)
【解析】分析:(1)通过配方得到;(2)先把抛物线的解析式写成交点式得到=(x-1)(x-5),即可得到抛物线与x轴的交点坐标;把x=0代入原函数关系式可确定抛物线与y轴的交点坐标.
本题解析:(1);
(2)∵=(x-1)(x-5),
∴抛物线与x轴交点坐标为(1,0),(5,0);
令x=0,y=-5,
故抛物... 下列关于x的方程中,不是分式方程的是( )
A. 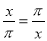 B.
B. 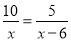 C.
C. 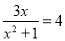 D.
D. 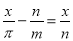
 D
【解析】A、分母中含有未知数,是分式方程,故本选项不符合题意;
B、分母中含有未知数,是分式方程,故本选项不符合题意;
C、分母中含有未知数,是分式方程,故本选项不符合题意;
D、分母中不含有未知数,不是分式方程,故本选项符合题意,
故选D.
D
【解析】A、分母中含有未知数,是分式方程,故本选项不符合题意;
B、分母中含有未知数,是分式方程,故本选项不符合题意;
C、分母中含有未知数,是分式方程,故本选项不符合题意;
D、分母中不含有未知数,不是分式方程,故本选项符合题意,
故选D. 二次函数y=ax2+bx+c满足b2=ac,且x=0时,y=﹣4,则( )
A. y最大=﹣4 B. y最小=﹣4 C. y最大=﹣3 D. y最小=﹣3
 C
【解析】试题分析:将x=0,y=-4代入可得:c=-4,根据可得: ,故函数有最大值,则最大值为: ,故选C.
C
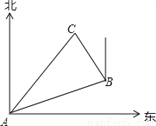
【解析】试题分析:将x=0,y=-4代入可得:c=-4,根据可得: ,故函数有最大值,则最大值为: ,故选C. 如图,在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点10千米的C地去,先沿北偏东70°方向走了8千米到达B地,然后再从B地走了6千米到达目的地C,此时小霞在B地的( )
A. 北偏东20°方向上 B. 北偏西20°方向上
C. 北偏西30°方向上 D. 北偏西40°方向上
 B
【解析】试题分析:根据题意可得:∠DAB=70°,AD∥BE,AC=10,AB=8,BC=6,根据勾股定理的逆定理可知∠ABC=90°,根据平行线的性质可得:∠ABE=110°,则∠CBE=110°-90°=20°,即点C在点B的北偏西20°方向上.
B
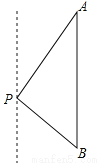
【解析】试题分析:根据题意可得:∠DAB=70°,AD∥BE,AC=10,AB=8,BC=6,根据勾股定理的逆定理可知∠ABC=90°,根据平行线的性质可得:∠ABE=110°,则∠CBE=110°-90°=20°,即点C在点B的北偏西20°方向上. 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
A. 40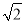 海里 B. 40
海里 B. 40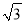 海里 C. 80海里 D. 40
海里 C. 80海里 D. 40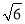 海里
海里
 A
【解析】试题分析:过点P作PD⊥AB于点D,根据方位角可得:∠A=30°,∠B=45°,根据AP=80海里可得PD=40海里,PB=40海里,故选A.
A
【解析】试题分析:过点P作PD⊥AB于点D,根据方位角可得:∠A=30°,∠B=45°,根据AP=80海里可得PD=40海里,PB=40海里,故选A. 如图,在□ABCD中,点M为CD的中点,且DC=2AD,则AM与BM的夹角的度数为( )
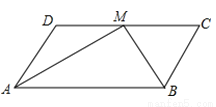
A. 100° B. 95° C. 90° D. 85°
 C
【解析】试题解析: 中,
∴DC∥AB,AD∥BC,
∴∠DAB+∠CBA=180°,∠BAM=∠DMA,
∵点M为CD的中点,且DC=2AD,
∴DM=AD,
∴∠DMA=∠DAM,
∴∠DAM=∠BAM,
同理∠ABM=∠CBM,
即:
∴∠AMB=180°-90°=90°.
故选C.
C
【解析】试题解析: 中,
∴DC∥AB,AD∥BC,
∴∠DAB+∠CBA=180°,∠BAM=∠DMA,
∵点M为CD的中点,且DC=2AD,
∴DM=AD,
∴∠DMA=∠DAM,
∴∠DAM=∠BAM,
同理∠ABM=∠CBM,
即:
∴∠AMB=180°-90°=90°.
故选C. 若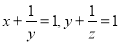 ,则
,则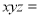 _____.
_____.
 -1
【解析】根据得: .
故答案:-1.
-1
【解析】根据得: .
故答案:-1. 
