题目内容
10．抛物线y=x2-3x+2与y轴交点的坐标为（ ）| A． | （0，2） | B． | （1，0） | C． | （2，0） | D． | （0，-3） |
分析 根据y轴上点的横坐标为0计算即可．
解答 解：对于y=x2-3x+2，
当x=0时，y=2，
则抛物线y=x2-3x+2与y轴交点的坐标为（0，2），
故选：A．
点评 本题考查的是二次函数图象上点的坐标特征，掌握y轴上点的坐标特点是解题的关键．
练习册系列答案
相关题目
5．
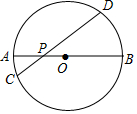如图，AB是⊙O的直径，弦CD交AB于点P，AP=2，BP=6，∠APC=30°，则CD的长为（ ）
如图，AB是⊙O的直径，弦CD交AB于点P，AP=2，BP=6，∠APC=30°，则CD的长为（ ）| A． | $\sqrt{15}$ | B． | 2$\sqrt{5}$ | C． | 2$\sqrt{15}$ | D． | 8 |
18．若代数式（A-$\frac{3}{a-1}$）•$\frac{2a-2}{a+2}$的化简结果为2a-4．则整式A为（ ）
| A． | a+1 | B． | a-1 | C． | -a-1 | D． | -a+1 |
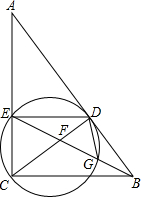如图，在Rt△ABC中，∠ACB=90°，点D是AB上一点，以CD为直径作⊙O，交AC于点E，连接BE分别交CD和⊙O于点F，G，连接DE，DG，且∠BDG=∠BED．
2．下列计算正确的是（ ）
| A． | 3x-2x=1 | B． | （-a3）2=-a6 | C． | x6÷x2=x3 | D． | x3•x2=x5 |
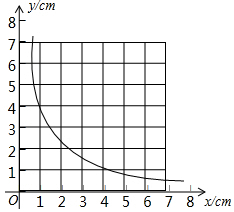一个三角形的面积始终保持不变，它的一边的长为xcm，这边上的高为ycm，y与x的关系如图，根据图中给出的信息，解答下列问题：
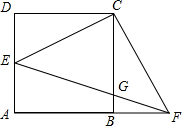如图，四边形ABCD是边长为1的正方形，点E在AD边上运动，且不与点A和点D重合，连结CE，过点C作CF⊥CE交AB的延长线于点F，EF交BC于点G．