题目内容
15.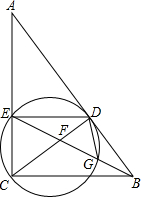 如图,在Rt△ABC中,∠ACB=90°,点D是AB上一点,以CD为直径作⊙O,交AC于点E,连接BE分别交CD和⊙O于点F,G,连接DE,DG,且∠BDG=∠BED.
如图,在Rt△ABC中,∠ACB=90°,点D是AB上一点,以CD为直径作⊙O,交AC于点E,连接BE分别交CD和⊙O于点F,G,连接DE,DG,且∠BDG=∠BED.(1)判断AB与⊙O的位置关系,并说明理由;
(2)若BE平分∠ABC,且CF=$\sqrt{2}$,求EF的长.
分析 (1)欲证明AB是⊙O的切线,只要证明CD⊥AB即可;
(2)设BC交⊙O于Q,作CP⊥EF于P.设EF=a,先证明DE=DB=CQ,设CQ=x,BC=y,由△BDQ∽△BCD,可得BD2=BQ•BC,可得x2=(y-x)y,解得$\frac{x}{y}$=$\frac{\sqrt{5}-1}{2}$(负根已经舍弃),由DE∥BC,可得$\frac{DE}{BC}$=$\frac{EF}{BF}$,推出BF=$\frac{2a}{\sqrt{5}-1}$,由△EPC∽△ECB,可得EC2=EP•EB,列出方程即可解决问题;
解答 解:(1)AB是⊙O的切线,
理由:∵CD为⊙O的直径,
∴∠CED=90°,
∵∠CEG=∠CDG,∠CEG+∠BED=90°,∠BDG=∠BED,
∴∠CDG+∠BDG=90°,
∴CD⊥AB,
∴AB是⊙O的切线;
(2)设BC交⊙O于Q,作CP⊥EF于P.设EF=a,
∵CD是直径,
∴∠CED=∠CQD=∠ECQ=90°,
∴四边形ECQD是矩形,
∴DE=CQ,
∵∠EBD=∠EBC=∠DEB,
∴DE=DB=CQ,设CQ=x,BC=y,
由△BDQ∽△BCD,可得BD2=BQ•BC,
∴x2=(y-x)y,
∴x2+xy-y2=0,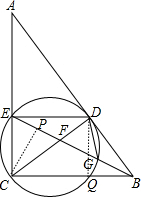
∴($\frac{x}{y}$)2+($\frac{x}{y}$)-1=0,
解得$\frac{x}{y}$=$\frac{\sqrt{5}-1}{2}$(负根已经舍弃),
∵DE∥BC,
∴$\frac{DE}{BC}$=$\frac{EF}{BF}$,
∴BF=$\frac{2a}{\sqrt{5}-1}$,
∵∠CEF+∠DEB=90°,∠DBF+∠DFB=90°,∠CFE=∠DFB,
∴∠CEF=∠CFE,
∴CE=CF,∵CP⊥EF,
∴EP=PF=$\frac{a}{2}$,
由△EPC∽△ECB,可得EC2=EP•EB,
∴($\sqrt{2}$)2=$\frac{a}{2}$•(a+$\frac{2a}{\sqrt{5}-1}$),
解得a=$\sqrt{5}$-1(负根已经舍弃),
∴EF=$\sqrt{5}$-1.
点评 本题考查切线的性质、角平分线的定义、矩形的判定和性质、相似三角形的判定和性质、一元二次方程等知识,解题的关键是学会添加辅助线,构造相似三角形解决问题,属于中考压轴题.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案| A. | (0,2) | B. | (1,0) | C. | (2,0) | D. | (0,-3) |
| A. | 2.24% | B. | -2.24% | C. | 2.24 | D. | -2.24 |
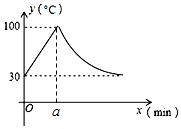 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图,
教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图,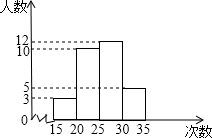 某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在30~35次之间的频率是( )
某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在30~35次之间的频率是( )