题目内容
2.解方程:(1)x2-2x-3=0;
(2)$\frac{2x}{x-2}$=1-$\frac{1}{2-x}$.
分析 (1)利用因式分解法解方程;
(2)先把方程化为整式方程,然后解整式方程后进行检验可确定原方程的解;
解答 解:(1)(x-3)(x+1)=0,
x-3=0或x+1=0,
所以x1=3,x2=-1;
(2)去分母得2x=x-2+1,
移项得2x-x=-2+1,
合并得x=-1,
经检验x=-1是原方程的解,
点评 本题考查了解一元二次方程-因式分解法:就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了解分式方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.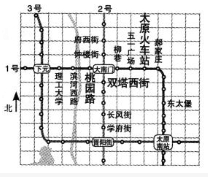 如图是利用正方形网格画出的太原市地铁1,2,3号线路部分规划示意图,若建立平面直角坐标系,表示太原火车站的点的坐标是(3,0),表示府西征街站的点的坐标是(0,2),则表示双塔西征街站(正好在两条网格线的交点上)的点坐标为( )
如图是利用正方形网格画出的太原市地铁1,2,3号线路部分规划示意图,若建立平面直角坐标系,表示太原火车站的点的坐标是(3,0),表示府西征街站的点的坐标是(0,2),则表示双塔西征街站(正好在两条网格线的交点上)的点坐标为( )
 如图是利用正方形网格画出的太原市地铁1,2,3号线路部分规划示意图,若建立平面直角坐标系,表示太原火车站的点的坐标是(3,0),表示府西征街站的点的坐标是(0,2),则表示双塔西征街站(正好在两条网格线的交点上)的点坐标为( )
如图是利用正方形网格画出的太原市地铁1,2,3号线路部分规划示意图,若建立平面直角坐标系,表示太原火车站的点的坐标是(3,0),表示府西征街站的点的坐标是(0,2),则表示双塔西征街站(正好在两条网格线的交点上)的点坐标为( )| A. | (0,1) | B. | (-3,-1) | C. | (0,-1) | D. | (-1,0) |
12.下列等式成立的是( )
| A. | (2a)2=2a2 | B. | (b3)m=b3m | C. | x2•x3=x6 | D. | x2+x2=x4 |