题目内容
12．已知关于x，y的二元一次方程组$\left\{\begin{array}{l}{ax+y=4}\\{x-by=3}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$，则ba=1．分析 把x与y的值代入方程组计算即可求出a与b的值．
解答 解：把$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$代入方程组得：$\left\{\begin{array}{l}{a+2=4}\\{1-2b=3}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$，
则原式=1，
故答案为：=1
点评 此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在矩形ABCD中，点E，F分别是AB，CD的中点，连结DE，BF，分别取DE，BF的中点M，N，连结AM，CN，MN，若AB=2$\sqrt{3}$，BC=2$\sqrt{5}$，则图中阴影部分图形的面积和为2$\sqrt{15}$．
3．在-1，$\frac{1}{3}$，$\sqrt{2}$，0.7中，无理数是（ ）
| A． | -1 | B． | $\frac{1}{3}$ | C． | $\sqrt{2}$ | D． | 0.7 |
如图，将△AOB绕点O按逆时针方向旋转45°后得到△COD，若∠AOB=15°，则∠AOD=30度．
7．
如图，△ABC的角平分线BE，CF相交于点O，且∠FOE=121°，则∠A的度数是（ ）
如图，△ABC的角平分线BE，CF相交于点O，且∠FOE=121°，则∠A的度数是（ ）| A． | 52° | B． | 62° | C． | 64° | D． | 72° |
17．
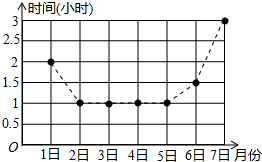“不怕同桌是学霸，就怕学霸放暑假．”如图是小明8月1日--7日每天在新华书店看书的时间统计图，则小明这七天平均每天在新华书店看书的时间是（ ）
“不怕同桌是学霸，就怕学霸放暑假．”如图是小明8月1日--7日每天在新华书店看书的时间统计图，则小明这七天平均每天在新华书店看书的时间是（ ）| A． | 1小时 | B． | 1.5小时 | C． | 2小时 | D． | 3小时 |
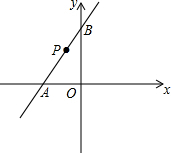如图，在平面直角坐标系中，已知直线y=kx+6与x轴、y轴分别交于A、B两点，且△ABO的面积为12．