Question

4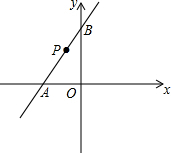． 如图，在平面直角坐标系中，已知直线y=kx+6与x轴、y轴分别交于A、B两点，且△ABO的面积为12．
（1）求k的值；
（2）若点P为直线AB的一动点，P点运动到什么位置时，△PAO使以OA为底的等腰三角形？求出此时点P的坐标；
（3）在（2）的条件下，坐标平面内是否存在点M，使以P、B、O、M为顶点组成的平行四边形为菱形？若存在，求出点M坐标；若不存在，试说明理由．

Answer 1

分析 （1）利用三角形的面积公式求出点A的坐标即可，利用待定系数法解决问题；
（2）当△PAO使以OA为底的等腰三角形时，P是AB的中点，利用中点坐标公式即可解决问题；
（3）分三种情形讨论即可解决问题；

解答 解：（1）∵y=kx+b，
∴B（0，6），
∴OB=6．
∵S_△ABO=12，
∴$\frac{1}{2}$•6•OA=12，
∴OA=4，
∴A（-4，0），
把A（-4，0）代入y=kx+6，可得k=$\frac{3}{2}$．

（2）∵△PAO使以OA为底的等腰三角形，
∴PA=PO，
∴∠PAO=∠POA，
∵∠PAO+∠ABO=90°，∠POA+∠POB=90°，
∴∠PBO=∠POB，
∴PB=PO，
∴PA=PB，
∵A（-4，0），B（0，6），
∴P（-2，3）．

（3）存在．
①如图1中，当四边形PBMO是平行四边形时，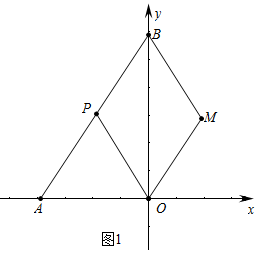

∵PB=PO，
∴四边形PBMO是菱形，易知P、M关于y轴对称，
∴M（2，3）．
②如图2中，当四边形PBOM是平行四边形时，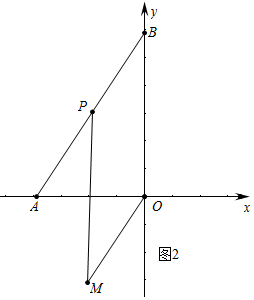

∵PB≠OB，
∴平行四边形PBMO表示菱形．
③如图3中，当四边形OPMB是平行四边形时，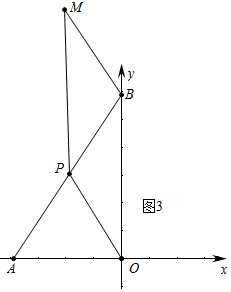

∵OP≠OB，
∴四边形OPMB表示菱形．
综上所述，满足条件的点M的坐标为（2，3）．

点评 本题考查一次函数综合题、待定系数法、平行四边形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题，属于中考常考题型．