题目内容
4.(1)计算:$\sqrt{12}$+(π-2016)0+($\frac{1}{2}$)-1-6tan30°;(2)解不等式组:$\left\{\begin{array}{l}2-3(x-3)≤5\\ \frac{1+2x}{3}>x-1\end{array}$,并把解集在数轴上表示出来.
分析 (1)直接根据二次根式的化简、零指数幂、负指数幂以及特殊角的三角函数值的知识求解即可求得答案;
(2)分别解不等式,然后在数轴上表示出来,继而求得答案.
解答 解:(1)原式=2$\sqrt{3}$+1+2-6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$+3-2$\sqrt{3}$=3;
(2)$\left\{\begin{array}{l}{2-3(x-3)≤5①}\\{\frac{1+2x}{3}>x-1②}\end{array}\right.$,
由①得:x≥2,
由①得:x<4,
把解集在数轴上表示得:
∴不等式组的解集为:2≤x<4.
点评 此题考查了实数的计算与不等式组的解法.注意掌握零指数幂、负指数幂以及特殊角的三角函数值的意义是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,四边形ABCD中,AD∥BC,AB⊥BC,点E在边AB上.
如图,四边形ABCD中,AD∥BC,AB⊥BC,点E在边AB上.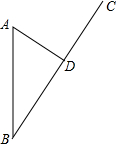 2016年9月中旬,全球最强台风“莫兰蒂”登陆福建,A市接到台风警报时,台风中心位于A市正南方向的B处,正以15km/h的速度沿BC方向移动.已知A市到BC的距离AD=30km,如果在距离台风中心45km(包括45km)的区域内都将受到台风影响,试问A市受到台风影响的时间是多长?( 结果精确到0.01h,参考数值:$\sqrt{5}$≈2.236 )
2016年9月中旬,全球最强台风“莫兰蒂”登陆福建,A市接到台风警报时,台风中心位于A市正南方向的B处,正以15km/h的速度沿BC方向移动.已知A市到BC的距离AD=30km,如果在距离台风中心45km(包括45km)的区域内都将受到台风影响,试问A市受到台风影响的时间是多长?( 结果精确到0.01h,参考数值:$\sqrt{5}$≈2.236 )
 如图,已知△ABC.
如图,已知△ABC. 我们可以用几何图形来解释一些代数恒等式,如图可以用来解释(a+b)2=a2+2ab+b2
我们可以用几何图形来解释一些代数恒等式,如图可以用来解释(a+b)2=a2+2ab+b2