题目内容
2.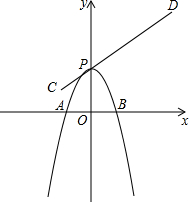 如图,抛物线与x轴相交于A、B两点,在保持抛物线的形状与大小不变的前提下,顶点P在线段CD上移动,点C、D的坐标分别为(-1,1)和(3,4).当顶点P移动到点C时,点B恰好与原点重合.在整个移动过程中,点A移动的距离为( )
如图,抛物线与x轴相交于A、B两点,在保持抛物线的形状与大小不变的前提下,顶点P在线段CD上移动,点C、D的坐标分别为(-1,1)和(3,4).当顶点P移动到点C时,点B恰好与原点重合.在整个移动过程中,点A移动的距离为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 通过“当顶点P移动到点C时,点B恰好与原点重合.”可以算出此时抛物线的解析式,由此可找出此时A点所在的位置记为A1,由于在整个运动中保持抛物线的形状与大小不变,即保持a不变,算出抛物线顶点在D点时抛物线的解析式,可以得出此时A点所在的位置记为A2,当P在CD上运动时,A在A1A2上运动,由此可得出结论.
解答 解:抛物线顶点在点C(-1,1)时,故设此时的抛物线解析式为y=a(x+1)2+1.
∵此时原点(0,0)在抛物线上,
∴有0=a(0+1)2+1,即a+1=0,解得a=-1,
∴抛物线的解析式为y=-(x+1)2+1.
令y=0,即-(x+1)2+1=0,
解得x1=-2,x2=0,
即此时A1点的坐标为(-2,0).
∵保持抛物线的形状与大小不变,即保持a不变,
∴当抛物线顶点运动到点D(3,4)时,此时抛物线解析式为y=-(x-3)2+4.
令y=0,即-(x-3)2+4=0,
解得x3=1,x4=5,
即此时A2点的坐标为(1,0).
∵抛物线顶点P在线段CD上移动,
∴A点在A1A2上运动,
∴在整个移动过程中,点A移动的距离为1-(-2)=3.
故选C.
点评 本题考查了二次函数的综合运用,解题的关键是:根据“保持抛物线的形状与大小不变”即保持a不变,由P与C重合时,B与原点重合,可求出a值.

练习册系列答案
相关题目
12.如果x=-1,y=2,那么式子$\frac{(x-y)^{3}}{{x}^{3}-{y}^{3}}$的值是( )
| A. | 1 | B. | 3 | C. | $\frac{1}{9}$ | D. | $\frac{1}{7}$ |
 如图,矩形ABCD中,AB=5,BD=13,Rt△EFG的直角边GE在CB的延长线上,E点与矩的B点重,∠FGE=90°,FG=3.将矩形ABCD固定,把Rt△EFG沿着射线BC方向运动,当点F恰好经过BD时,将△EFG绕点F逆时针旋转α°(0°<α°<90°),记旋转中的△EFG为△E′F′G′,在旋转过程中,设直线E′G′与直线BC交于N,与直线BD交于M点,当△BMN为以MN为底边的等腰三角形时,FM的长为3$\sqrt{26}$.
如图,矩形ABCD中,AB=5,BD=13,Rt△EFG的直角边GE在CB的延长线上,E点与矩的B点重,∠FGE=90°,FG=3.将矩形ABCD固定,把Rt△EFG沿着射线BC方向运动,当点F恰好经过BD时,将△EFG绕点F逆时针旋转α°(0°<α°<90°),记旋转中的△EFG为△E′F′G′,在旋转过程中,设直线E′G′与直线BC交于N,与直线BD交于M点,当△BMN为以MN为底边的等腰三角形时,FM的长为3$\sqrt{26}$.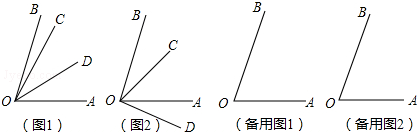
 如图,已知直线y=x+3与x轴交于点A,与y轴交于点B.抛物线y=-x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E.
如图,已知直线y=x+3与x轴交于点A,与y轴交于点B.抛物线y=-x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E. 已知如图:Rt△ABC中,∠ACB=90°,AE平分∠BAC,BD平分∠ABC,AE、BD相交于O,OF⊥BD,OH⊥AB.
已知如图:Rt△ABC中,∠ACB=90°,AE平分∠BAC,BD平分∠ABC,AE、BD相交于O,OF⊥BD,OH⊥AB.