题目内容
17.已知a,b为有理数,m,n分别表示5-$\sqrt{7}$的整数部分和小数部分,且am+bn=0,求代数式$\frac{a}{2b}$+$\frac{3}{4}$的值.分析 根据已知首先求出m,n的值,进而化简原式得出2a+3b=0,b=0,求出即可.
解答 解:∵m,n分别表示5-$\sqrt{7}$的整数部分和小数部分,
∴m=2,n=5-$\sqrt{7}$-2=3-$\sqrt{7}$,
∴am+bn=a×2+(3-$\sqrt{7}$)b=2a+(3-$\sqrt{7}$)b=0,
∴$\frac{a}{b}=\frac{\sqrt{7}-3}{2}$
∴$\frac{a}{2b}$+$\frac{3}{4}$=$\frac{1}{2}×\frac{\sqrt{7}-3}{2}+\frac{3}{4}$=$\frac{\sqrt{7}}{4}$.
点评 本题考查了估算无理数的大小,解决本题的根据是求出m,n的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.用配方法解方程x2+4x=3,下列配方正确的是( )
| A. | (x-2)2=1 | B. | (x-2)2=7 | C. | (x+2)2=7 | D. | (x+2)2=1 |
9.下列图形中,将图形上各点的纵坐标保持不变,横坐标分别乘-1后,图形的形状一定不发生变化的是( )
(1)圆心在原点的圆;(2)两条对角线的交点在原点的正方形;(3)以y轴为对称轴的等腰三角形;(4)以x轴为对称轴的等腰三角形.
(1)圆心在原点的圆;(2)两条对角线的交点在原点的正方形;(3)以y轴为对称轴的等腰三角形;(4)以x轴为对称轴的等腰三角形.
| A. | (1)(2)(3)(4) | B. | (1)(2)(4) | C. | (1)(3) | D. | (2)(4) |
 如图,⊙O是△ABC的外接圆,⊙O的半径R=2,∠B=60°,则弦AC的长为2$\sqrt{3}$.
如图,⊙O是△ABC的外接圆,⊙O的半径R=2,∠B=60°,则弦AC的长为2$\sqrt{3}$.
 当投影线由物体的左方射到右方时,如图所示,几何体的正投影是( )
当投影线由物体的左方射到右方时,如图所示,几何体的正投影是( )



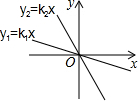 已知函数y=x;y=-2x.y=$\frac{1}{2}$x,y=3x.
已知函数y=x;y=-2x.y=$\frac{1}{2}$x,y=3x.