题目内容
8.数学实验室:制作4张全等的直角三角形纸片(如图1),把这4张纸片拼成以弦长c为边长的正方形构成“弦图”(如图2),古代数学家利用“弦图”验证了勾股定理.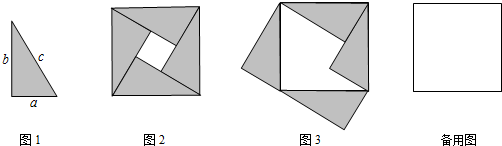
探索研究:
(1)小明将“弦图”中的2个三角形进行了旋转,得到图3,请利用图3证明勾股定理;
数学思考:
(2)小芳认为用其它的方法改变“弦图”中某些三角形的位置,也可以证明勾股定理.请你想一种方法支持她的观点(先在备用图中补全图形,再予以证明).
分析 (1)通过图形的面积的两种计算方法,即可得出结果;
(2)通过大正方形面积的两种计算方法,即可得出结果.
解答 解:(1)如图3所示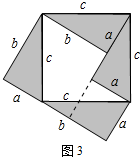
∵图形的面积表示为a2+b2+2×$\frac{1}{2}$ab=a2+b2+ab,
图形的面积也可表示为c2+4×$\frac{1}{2}$ab=c2+ab;
∴(a+b)2=c2+4×$\frac{1}{2}$ab,
a2+b2+ab=c2+ab,
∴a2+b2=c2
即直角三角形两直角边的平方和等于斜边的平方.
(2))如图4所示: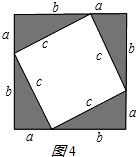
∵大正方形的面积表示为(a+b)2;
大正方形的面积也可表示为c2+4×$\frac{1}{2}$ab
∴(a+b)2=c2+4×$\frac{1}{2}$ab,
a2+b2+2ab=c2+2ab,
∴a2+b2=c2;
即直角三角形两直角边的平方和等于斜边的平方.
点评 此题考查了勾股定理的证明、正方形的性质、直角三角形面积的计算;关键是利用三角形和正方形边长的关系进行组合图形,利用面积的关系证明勾股定理.

练习册系列答案
相关题目
20.下列计算正确的是( )
| A. | $\sqrt{2}-\sqrt{2}$=0 | B. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | C. | $\sqrt{(-2)^{2}}$=-2 | D. | 4+$\sqrt{2}$=2 |
 如图,已知Rt△ABC中,∠ACB=90°,BC=12,AC=16,CD⊥AB于点D.求CD的长.
如图,已知Rt△ABC中,∠ACB=90°,BC=12,AC=16,CD⊥AB于点D.求CD的长.