题目内容
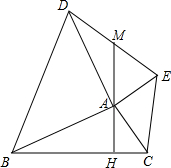 如图,在△ABC外作等腰直角△ABD与等腰直角△ACE,使得∠BAD=90°,∠CAE=90°,AH⊥BC,垂足为H,AH的反向延长线交DE于M,求证:DM=EM.
如图,在△ABC外作等腰直角△ABD与等腰直角△ACE,使得∠BAD=90°,∠CAE=90°,AH⊥BC,垂足为H,AH的反向延长线交DE于M,求证:DM=EM.考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:在BC上截取BF=AM,易证△ABF≌△ADM,可得DM=AF和∠DMA=∠BFA,即可求证△ACF≌△AEM,可得ME=AF,即可解题.
解答:证明:在BC上截取BF=AM,

∵∠BAD=∠CAE=∠AHB=∠AHC=90°,
∴∠BAH+∠ABC=∠BAH+∠DAM=∠CAH+∠BCA=∠CAH+∠EAM=90°,
∴∠CBA=∠DAM,∠BCA=∠EAM,
在△ABF和△ADM中,
,
∴△ABF≌△ADM,(SAS)
∴DM=AF,∠DMA=∠BFA,
∴∠EMA=∠CFA,
在△ACF和△AEM中,
,
∴△ACF≌△AEM(AAS),
∴GE=AF=GD.

∵∠BAD=∠CAE=∠AHB=∠AHC=90°,
∴∠BAH+∠ABC=∠BAH+∠DAM=∠CAH+∠BCA=∠CAH+∠EAM=90°,
∴∠CBA=∠DAM,∠BCA=∠EAM,
在△ABF和△ADM中,
|
∴△ABF≌△ADM,(SAS)
∴DM=AF,∠DMA=∠BFA,
∴∠EMA=∠CFA,
在△ACF和△AEM中,
|
∴△ACF≌△AEM(AAS),
∴GE=AF=GD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABF≌△ADM和△ACF≌△AEM是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
2012年恩施机场和火车站的客流总量达到824000人次,这个数用科学记数法表示为( )
| A、824×104 |
| B、8.24×105 |
| C、8.24×106 |
| D、0.824×107 |
 如图,△ABC中,M为AC边的中点,E为AB上一点,且AE=
如图,△ABC中,M为AC边的中点,E为AB上一点,且AE=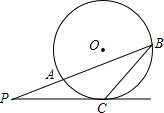 如图,已知P是⊙O外一点,从P引两条射线,分别与⊙O交于A、B及C,且PC2=PA•PB,求证:PC是⊙O的切线.
如图,已知P是⊙O外一点,从P引两条射线,分别与⊙O交于A、B及C,且PC2=PA•PB,求证:PC是⊙O的切线.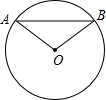 如图,已知⊙O的半径为30mm,弦AB=36mm,求点O到AB的距离及∠OAB的余弦值.
如图,已知⊙O的半径为30mm,弦AB=36mm,求点O到AB的距离及∠OAB的余弦值.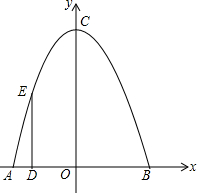 《西游记》中的孙悟空对花果山的体制进行全面改革后,为了改善旅游环境,决定对水帘洞改造翻新,计划在水帘洞前建一个由喷泉组成的水帘门洞,让游客在进入水帘洞前先经过一段由鹅卵石铺就的小道,小道两旁布满喷水管,每个喷水管喷出的水最高达4米,落在地上时距离喷水管4米.现在设如图是喷泉所经过的路线,以喷头A和喷泉落地点B的连线所在直线为横轴,AB的垂直平分线为纵轴建立平面直角坐标系.问小道的边缘距离喷水管至少应为多少米,才能使身高不高于1.75米的游客进入水帘洞时不会被水淋湿?
《西游记》中的孙悟空对花果山的体制进行全面改革后,为了改善旅游环境,决定对水帘洞改造翻新,计划在水帘洞前建一个由喷泉组成的水帘门洞,让游客在进入水帘洞前先经过一段由鹅卵石铺就的小道,小道两旁布满喷水管,每个喷水管喷出的水最高达4米,落在地上时距离喷水管4米.现在设如图是喷泉所经过的路线,以喷头A和喷泉落地点B的连线所在直线为横轴,AB的垂直平分线为纵轴建立平面直角坐标系.问小道的边缘距离喷水管至少应为多少米,才能使身高不高于1.75米的游客进入水帘洞时不会被水淋湿?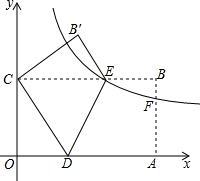 如图,在平面直角坐标系中,A(16,0)、C(0,8),四边形OABC是矩形,D、E分别是OA、B才边上的点,沿着DE折叠矩形,点A恰好落在y轴上的点C处,点B落在点B′处.
如图,在平面直角坐标系中,A(16,0)、C(0,8),四边形OABC是矩形,D、E分别是OA、B才边上的点,沿着DE折叠矩形,点A恰好落在y轴上的点C处,点B落在点B′处.
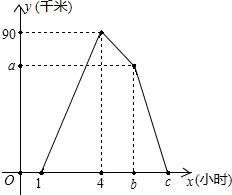 甲、乙两人同时从家乘车去县城,途中甲因故下车,改骑自行车前往县城(换车的时间不计).已知甲骑自行车的速度为15千米/小时,乙到达县城停留1小时后,以另一速度返回,1小时后与甲相遇.如图为甲、乙两人之间的距离y(千米)与行驶时间x(小时)之间的函数关系.
甲、乙两人同时从家乘车去县城,途中甲因故下车,改骑自行车前往县城(换车的时间不计).已知甲骑自行车的速度为15千米/小时,乙到达县城停留1小时后,以另一速度返回,1小时后与甲相遇.如图为甲、乙两人之间的距离y(千米)与行驶时间x(小时)之间的函数关系.