题目内容
 已知:如图,AD是△ABC的角平分线,过D点分别作AC和AB的平行线,交AB于点E,交AC于点F.
已知:如图,AD是△ABC的角平分线,过D点分别作AC和AB的平行线,交AB于点E,交AC于点F.(1)求证:四边形AEDF是菱形.
(2)当∠BAC=
考点:菱形的判定,正方形的判定
专题:
分析:(1)首先根据题意可得四边形AEDF是平行四边形,然后再证明AE=ED,根据邻边相等的平行四边形是菱形可得结论;
(2)添加∠BAC=90°,根据有一个角是直角的菱形是正方形可得菱形AEDF是正方形.
(2)添加∠BAC=90°,根据有一个角是直角的菱形是正方形可得菱形AEDF是正方形.
解答:
(1)证明:∵过D点分别作AC和AB的平行线,交AB于点E,交AC于点F,
∴DE∥AF,DF∥AE,
∴四边形AEDF是平行四边形,
又∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠EDA=∠DAC,
∴∠BAD=∠EDA,
∴AE=ED
∴四边形AEDF为菱形;
(2)解:当∠BAC=90°时,菱形AEDF是正方形.
故答案为:90.
∴DE∥AF,DF∥AE,
∴四边形AEDF是平行四边形,
又∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠EDA=∠DAC,
∴∠BAD=∠EDA,
∴AE=ED
∴四边形AEDF为菱形;
(2)解:当∠BAC=90°时,菱形AEDF是正方形.
故答案为:90.
点评:此题主要考查了菱形的判定和正方形的判定,关键是掌握邻边相等的平行四边形是菱形,有一个角是直角的菱形是正方形.

练习册系列答案
相关题目
已知(-2,y1),(-1,y2),(3,y3)是二次函数y=x2-4x+m上的点,则y1,y2,y3的大小关系( )
| A、y1<y2<y3 |
| B、y2<y1<y3 |
| C、y1<y3<y2 |
| D、y3<y2<y1 |
 如图,已知抛物线y=x2-3x经过B(4,4).将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标.
如图,已知抛物线y=x2-3x经过B(4,4).将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标. 如图所示,点P在直线l上,或者说直线l
如图所示,点P在直线l上,或者说直线l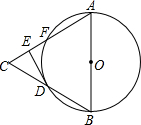 如图,在等边三角形△ABC中,以AB为直径的⊙O交BC于点D,交AC于点F,过D作⊙O的切线交AC于E.若DE=2,则⊙O的面积等于
如图,在等边三角形△ABC中,以AB为直径的⊙O交BC于点D,交AC于点F,过D作⊙O的切线交AC于E.若DE=2,则⊙O的面积等于 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=100°,若点E在弧AD上,则∠E的度数为
如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=100°,若点E在弧AD上,则∠E的度数为